双曲线 的一条渐近线方程是 ( )
的一条渐近线方程是 ( )
A.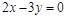 |
B.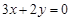 |
C.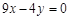 |
D. |
设  ,则
,则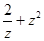 =( )
=( )
| A.-1-i | B.1-I | C.-l+i | D.l+i |
命题“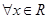 ,
,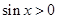 ”的否定是
”的否定是
A.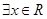 , ,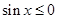 |
B.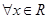 , ,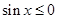 |
C.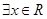 , ,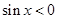 |
D.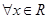 , ,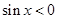 |
若 则“
则“ ”是“方程
”是“方程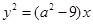 表示开口向右的抛物线”的( )
表示开口向右的抛物线”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“a≠1或b≠2”是“a+b≠3”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
与椭圆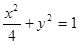 共焦点且过点
共焦点且过点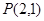 的双曲线方程是( )
的双曲线方程是( )
A.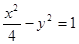 |
B. |
C. |
D. |
【原创】已知复数 ,且
,且 ,则双曲线
,则双曲线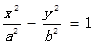 的离心率为( )
的离心率为( )
A. |
B.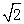 |
C.2 | D.3 |
方程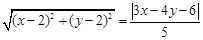 表示的曲线为( )
表示的曲线为( )
| A.抛物线 | B.椭圆 | C.双曲线 | D.圆 |
【改编】已知函数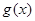 是偶函数,
是偶函数, ,其导函数
,其导函数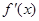 满足
满足 ,则 ( )
,则 ( )
A. |
B.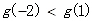 |
C. |
D. |
已知直线 是曲线
是曲线 的一条切线,则
的一条切线,则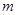 的值为( )
的值为( )
A. |
B. |
C.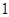 |
D. |
对具有线性相关关系的变量x,y有一组观测数据(xi,yi)( i=1,2,…,8),其回归直线方程是 =
=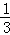 x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
A.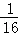 |
B.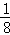 |
C.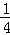 |
D. |
已知函数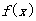 的导函数
的导函数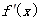 的图象如图所示,
的图象如图所示, ,令
,令
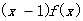 ,
,
则不等式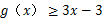 的解集是( )
的解集是( )

A. |
B.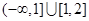 |
C.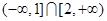 |
D.[-1,2] |
下列推理中属于归纳推理且结论正确的是( )
| A.由an=2n﹣1,求出S1=12,S2=22,S3=32,…,推断:数列{an}的前n项和Sn=n2 |
B.由f(x)=xcosx满足f(﹣x)=﹣f(x)对 都成立,推断:f(x)=xcosx为奇函数 都成立,推断:f(x)=xcosx为奇函数 |
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆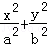 =1的面积S=πab =1的面积S=πab |
D.由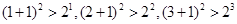 ,…,推断:对一切 ,…,推断:对一切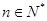 ,(n+1)2>2n ,(n+1)2>2n |
设复数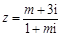 (
(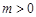 ,i为虚数单位),若
,i为虚数单位),若 ,则
,则 的值为 .
的值为 .
设函数f(x)= (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))=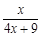 , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))=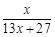 , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
【改编】若函数 在其定义域内的一个子区间
在其定义域内的一个子区间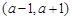 内为单调函数,则实数
内为单调函数,则实数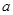 的取值范围 .
的取值范围 .
已知函数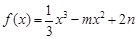 (
(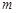 ,
, 为常数),当
为常数),当 时,函数
时,函数 有极值,若函数
有极值,若函数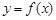 有且只有三个零点,则实数
有且只有三个零点,则实数 的取值范围是 .
的取值范围是 .
设复数z=-3cosθ+2isinθ.
(1)当θ=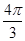 时,求|z|的值;
时,求|z|的值;
(2)若复数z所对应的点在直线x+3y=0上,求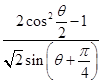 的值.
的值.
(本小题满分10分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
| 分数段 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出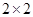 列联表,并判断是否有
列联表,并判断是否有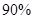 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
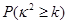 |
0.100 |
0.050 |
0.010 |
0.001 |
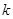 |
2.706 |
3.841 |
6.635 |
10.828 |
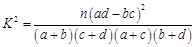 .
.
【改编】(本小题满分10分)已知函数 .
.
(1)求函数的单调增区间;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
【原创】
(1)观察下列各式;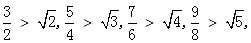 根据以上各式利用归纳推理得出一个一般性的结论;
根据以上各式利用归纳推理得出一个一般性的结论;
(2)设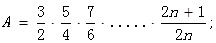
 根据
根据 的大小关系证明(1)的结论;
的大小关系证明(1)的结论;