“
”是“
”的
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
双曲线
-
=1的焦点到渐近线的距离为（ ）
A． |
B．2 | C． |
D．1 |
原命题“若
，则
”的逆否命题是
A．若 ，则 |
B．若 ，则 |
| C．若，则 |
D．若，则 |
已知命题
则
是（ ）
A． |
B． |
C． |
D． |
若
（ ）
A． |
B． |
C． |
D． |
【原创】某中校为方便家长与学校联系，在办公楼的楼厅墙上张贴一副图如下，下面叙述正确的是（ ）
| A．教务处的直接领导是校长 |
| B．教学副校长的直接下属有督导处 |
| C．这是一个流程图 |
| D．这是一个结构图 |
【改编】设函数
，则（ ）
A． 的减区间为 |
B． 为的极小值点 |
| C．为的极大值点 |
| D．有最大值 |
【改编】定义在
上的函数
，
是它的导函数，且恒有
成立，则（ ）
A． |
B． |
C． |
D． |
（某部门为了了解青年人喜欢户外运动是否与性别有关，运用2×2列联表进行独立性检验，经计算K2=7．069，则所得到的统计学结论为：有（ ）把握认为“喜欢户外运动与性别有关”．
附：（独立性检验临界值表）
| P（K2≥k0） |
0．05 |
0．025 |
0．010 |
0．005 |
0．001 |
| k0 |
3．841 |
5．024 |
6．636 |
7．879 |
10．828 |
A．0．1% B．1% C．99% D．99．9%
【改编】算法的程序框图如图，若输入的
， 则输出的
的值为（ ）
A． |
B． |
C．1 | D．4 |
【改编】看图表①--④，下列叙述正确的是（ ）
①．
②．
| A．①为流程图 | B．②流程图 | C．流程图是静态的 | D．结构图是动态的 |
【原创】已知：
是函数
的两个极值点，且
，则直线
与椭圆
的位置关系为（ ）
| A．相切 | B．相交 | C．相离 | D．位置关系不确定 |
已知f（x）=x2+2x•f′（1），则f′（0）= ．
已知下列四个等式
依此类推，猜想第
个等式为 ．
已知P是椭圆
上不同于左顶点A、右顶点B的任意一点，记直线PA，PB的斜率分别为
的值为 ．
【改编】已知函数f（x）＝－
x2＋4x－3ln x在
上单调，则t的取值范围是________．
已知
是复数，若
为实数（
为虚数单位），且
为纯虚数．
（1）求复数；
（2）若复数
在复平面上对应的点在第四象限，求实数
的取值范围
【改编】已知函数
在
与
时都取得极值
（1）求
的值与函数
的单调区间
（2）若
，且存在
，不等式
恒成立，求m的取值范围．
（本小题满分10分）已知函数
，
．
（1）讨论
的单调区间；
（2）当
时，求在
上的最小值，并证明
．
（本小题满分10分）在平面直角坐标系xOy中，椭圆C：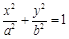
（a＞b＞0）的上顶点到焦点的距离为2，离心率为
．
（1）求a，b的值．
（2）设P是椭圆C长轴上的一个动点，过点P作斜率为k的直线l交椭圆C于A、B两点．
（ⅰ）若k＝1，求△OAB面积的最大值；
（ⅱ）若PA2＋PB2的值与点P的位置无关，求k的值．