已知角 的终边与单位圆交于点P(x,y),则( )
的终边与单位圆交于点P(x,y),则( )
A. |
B. |
C. |
D. |
【原创】如果角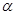 的终边过点
的终边过点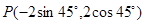 ,则
,则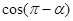 的值等于( )
的值等于( )
A.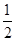 |
B.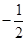 |
C.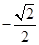 |
D.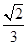 |
若 是钝角,则
是钝角,则 是( )
是( )
| A.第二象限角 |
| B.第三象限角 |
| C.第二象限角或第三象限角 |
| D.第二象限角或第四象限角 |
扇形圆心角为 ,半径为
,半径为 ,则扇形内切圆的圆面积与扇形面积之比为( )
,则扇形内切圆的圆面积与扇形面积之比为( )
| A.1∶3 | B.2∶3 | C.4∶3 | D.4∶9 |
【原创】已知△ABC中, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
用“五点法”作y=2sin2x的图象时,首先描出的五个点的横坐标是( )
A. |
B. |
| C.0,π,2π,3π,4π | D. |
已知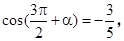 且α是第四象限角,则cos(-3π+α)=( )
且α是第四象限角,则cos(-3π+α)=( )
A.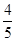 |
B.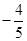 |
C.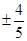 |
D.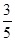 |
设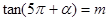 ,则
,则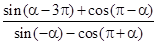 的值等于( )
的值等于( )
A.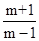 |
B.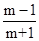 |
C.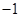 |
D.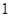 |
【原创】函数y=tan( )的定义域是( )
)的定义域是( )
A.{x|x≠ x∈R} x∈R} |
B.{x|x≠ x∈R} x∈R} |
C.{x|x≠ k∈Z,x∈R} k∈Z,x∈R} |
D.{x|x≠ k∈Z,x∈R} k∈Z,x∈R} |
单摆从某点开始来回摆动,离开平衡位置O的距离s cm和时间t s的函数关系式为s=6sin(2πt+ ),那么单摆来回摆动一次所需的时间为( )
),那么单摆来回摆动一次所需的时间为( )
| A.2π s | B.π s | C.0.5 s | D.1 s |
函数y= 的图象与x轴各个交点中离原点最近的一点是( )
的图象与x轴各个交点中离原点最近的一点是( )
A.( ,0) ,0) |
B.( ,0) ,0) |
C.( ,0) ,0) |
D.( ,0) ,0) |
设函数 满足
满足 ,则函数
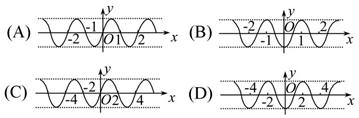
,则函数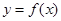 的图象是( )
的图象是( )
点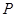 从点
从点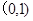 出发,沿单位圆
出发,沿单位圆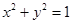 逆时针方向运动
逆时针方向运动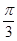 弧长到达
弧长到达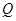 点,则
点,则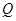 的坐标为_.
的坐标为_.
【改编题】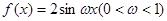 ,在区间
,在区间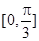 上的最大值是
上的最大值是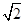 ,则ω=________.
,则ω=________.
如图所示是一弹簧振子做简谐振动的图象,横轴表示振动的时间,纵轴表示振子的位移,则这个振子振动的函数解析式是_______.
【原创】给出下列说法:
①函数y=cosx在第三、四象限都是增函数;②函数y=tan(ωx+φ)的最小正周期为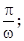
③函数y=sin(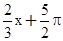 )是偶函数;④函数y=tan2x的图象向左平移
)是偶函数;④函数y=tan2x的图象向左平移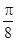 个单位长度得到y=tan(
个单位长度得到y=tan(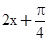 )的图象.其中正确说法的序号是_______.
)的图象.其中正确说法的序号是_______.
(本小题满分12分)化简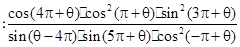
【原创】(本小题满分12分)已知扇形OAB的圆心角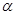 为120°,半径长为6,
为120°,半径长为6,
(1)求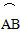 的弧长;(2)求弓形OAB的面积.
的弧长;(2)求弓形OAB的面积.
(本小题满分12分)当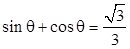 时,求
时,求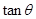 的值.
的值.
(本小题满分12分)设函数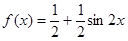 .
.
(1)求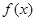 的最小正周期;
的最小正周期;
(2)设函数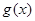 对任意x∈R,有
对任意x∈R,有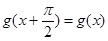 ,且当
,且当 时,
时,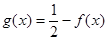 ,求
,求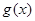 在区间
在区间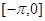 上的解析式.
上的解析式.
【原创】已知函数 在某一个周期内的图像的最高点和最低点的坐标分别为
在某一个周期内的图像的最高点和最低点的坐标分别为
(1)求A和ω的值;(2)已知 ,且
,且 ,求
,求 的值.
的值.
(本小题满分12分)已知函数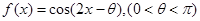 的图像过点
的图像过点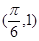 .
.
(1)求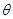 的值;
的值;
(2)将函数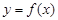 图像上各点的横坐标变为原来的2倍,纵坐标不变,得到函数
图像上各点的横坐标变为原来的2倍,纵坐标不变,得到函数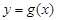 的图像,求函数
的图像,求函数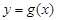 在
在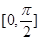 上的最大值和最小值.
上的最大值和最小值.