函数
在（ ）
A． 上是减函数 |
B． 上是增函数 |
C． 上是减函数 |
D． 上是减函数 |
若
为第二象限角，则
可化简为（ ）
A． |
B． |
C． |
D． |
【改编题】直线
与函数
的图像相交，则相邻两交点间的距离是（ ）
A． |
B． |
C． |
D． |
若点
在第一象限，则在
内
的取值范围是 （ ）
A． |
B． |
C． |
D． |
【改编题】设函数
为 （ ）
A．周期函数，最小正周期为 |
B．周期函数，最小正周期为 |
C．周期函数，最小正周期为 |
| D．非周期函数 |
函数
的值域是（ ）
A． |
B． |
C． |
D． |
若函数
，
的最小正周期为
，且
，则（ ）
A． ， |
B．， |
C． ， |
D．， |
【原创】下列函数中，对于任意
R，同时满足条件（1）图像关于
轴对称；（2）
的函数是（ ）
A． |
B． |
C． |
D． |
设函数
，则下列结论正确的是（ ）
A． 的图象关于点 对称 |
B． 的图象关于直线x= 对称 |
C． 的最小正周期为π |
D．在 上为增函数 |
使
在区间
至少出现2次最大值，则ω的最小值为（ ）
A． |
B． |
C． |
D． |
已知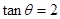
，则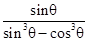
=（ ）
A． |
B． |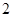
C． |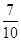
D． |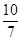
【原创】在△ABC中，若sin（A+B-C）=sin（A-B+C），则△ABC必是（ ）
（A）等腰三角形 （B）直角三角形
（C）等腰或直角三角形 （D）等腰直角三角形
函数的
定义域为___________。
【改编题】若函数
在区间
上单调递增，在区间
上单调递减，则
_____．
M、N是曲线y=πsinx与曲线y=πcosx的两个不同的交点，则|MN|的最小值为_____．
①存在
使
；
②存在区间
，使
为减函数，而
＜0；
③
在其定义域内为增函数；
④
最小正周期为π。
以上命题不正确的为_______。
已知cosα=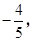
并且α是第二象限的角．
（1）求sinα和tanα的值；
（2）求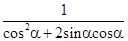
的值．
【原创】（本小题满分12分）求
的值。
（本小题满分12分）已知电流I与时间t的关系式为
．
（1）下图是
在一个周期内的图象，根据图中数据求的解析式；
（2）如果t在任意一段
秒的时间内，电流都能取得最大值和最小值，那么ω的最小正整数值是多少？
（本小题满分12分）已知函数f（x）=
sin（2ωx+φ）（ω＞0，φ∈（0，π））的图象中相邻两条对称轴间的距离为
，且点（
，0）是它的一个对称中心．
（1）求f（x）的表达式；
（2）若f（ax）（a＞0）在（0，
）上是单调递减函数，求a的最大值．
（本小题满分12分）如图，在平面直角坐标系xoy中，角α的始边与x轴的非负半轴重合且与单位圆相交于A点，它的终边与单位圆相交于x轴上方一点B，始边不动，终边在运动．
（1）若点B的横坐标为
，求tanα的值；
（2）若△AOB为等边三角形，写出与角α终边相同的角β的集合；
（3）若
，请写出弓形AB的面积S与α的函数关系式．
【原创】（本小题满分12分）已知把函数
的图像向右平移
个单位，在向上平移一个单位得到函数
的图像．
（1）求的最小值及取最小值时
的集合；
（2）求在
时的值域；（3）若
，求
的单调增区间。