下面图形中,表示北偏东60°的是( )
A. |
B. |
C. |
D. |
如图,小明在操场上从A点出发,先沿北偏西30°方向走到B点,再沿北偏东45°方向走到C点,这时∠ABC的度数是( )
| A.105° |
| B.75° |
| C.45° |
| D.165° |
点A的方向位于0点的( )
| A.北偏东25° |
| B.南偏西25° |
| C.北偏西65° |
| D.北偏东65° |
一轮船行驶到小岛A处,同时测得灯塔B、C分别在它的北偏西30°和东北方向,则∠BAC=( )
A. 105°
B. 115°
C. 75°
D. 95°
下列结论正确的是( )
| A.直线比射线长 |
| B.过两点有且只有一条直线 |
| C.过三点一定能作三条直线 |
| D.一条直线就是一个平角 |
在下列说法中,正确的是( )
①两条射线组成的图形叫做角;②角的大小与边的长短无关;
③角的两边可以一样长,也可以一长一短;④角的两边是两条射线.
| A.①② |
| B.②④ |
| C.②③ |
| D.③④ |
如图,能用∠1,∠ACB,∠C三种方法表示同一个角的是( )
A. |
B. |
C. |
D. |
下列各图中,射线OA表示北偏东42°方向的是( )
A. |
B. |
C. |
D. |
若∠A=30°18′,∠B=30°15′30″,∠C=30.25°,则这三个角的大小关系正确的是( )
| A.∠C>∠A>∠B |
| B.∠C>∠B>∠A |
| C.∠A>∠C>∠B |
| D.∠A>∠B>∠C |
点A在点B的北偏东60°方向上,点C在射线BA与正北方向夹角的角平分线上,那么点B测点C的方向是北偏东_______度.
如图,射线OA所表示的方向为_______.
如图中射线OA表示的方位角为_______.
如果小明看小亮的方向是北偏东30°,则小亮看小明的方向应是_______.
3100″=_______度
25.4度=_______度_______分_______秒.
若∠A=20°18′,∠B=20.25°,则∠A_______∠B(空内填“>”或“<”或“=”)
如图,要将角钢(图①)弯成145°(图②)的钢架,在角钢上截去的缺口(图①中的虚线)应为_______度.
比萨斜塔建成于12世纪,从建成之日起就一直倾斜.目前,它与地面所成的较小的角是85度,它与地面所成的较大的角是_______度.
2时32分时,时针与分针的夹角是_______度.
 周角=_______ 平角="_______" 直角.
周角=_______ 平角="_______" 直角.
点A位于点B的北偏东40°,那么点B位于点A的_______偏_______ 40°.
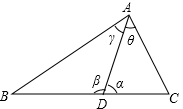
将图中的角用不同方法表示出来,并填写下表:
| |
∠α |
∠β |
∠C |
|
∠θ |
| ∠ABC |
|
|
|
∠BAD |
|
一只小虫从点A出发向北偏西30°方向爬行了3cm到点B,再从点B出发向北偏东60°方向爬行了3cm到点C,
(1)试画图确定A、B、C的位置;
(2)从图上量出点C到点A的距离.(精确到0.1cm)
(3)指出点C在点A的什么方位?
计算:
(1)将24.29度化为度、分、秒.
(2)将36度40分30秒化为度.
如图,一只蚂蚁从O点出发,沿北偏东30°方向爬行2.5cm,碰到障碍物B后,又沿西北方向爬行3cm到达C处.
(1)画出蚂蚁爬行的路线.
(2)求∠OBC的度数.
如图所示,从一点O出发引射线OA、OB、OC、OD,请你数一数图中有多少个角,并把它们表示出来.
如图,甲乙两船同时从A港出发,甲船沿北偏东35°的方向,以每小时12海里的速度向B岛驶去.乙船沿南偏东55°的方向向C岛驶去,2小时后,两船同时到达了目的地.若C、B两岛的距离为30海里,问乙船的航速是多少?
如图,A、B两地均为海上观测站,从A地发现它的西南方向上有一艘船,同时,从B地发现它在南偏东30°方向上,试在图中确定这艘船(用点M表示)的位置.
小明有一张地图,如图所示,上面标有A、B、C三地,由于被墨迹污染,C地的具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的东南方向,A地在B地的东偏南70°.
(1)请你在图中画一画,试着帮他确定C地在地图上的位置;
(2)求∠ABC的大小.