已知集合 ,
, ,且
,且 ,则实数
,则实数 的值是 .
的值是 .
若 ,则
,则 =________.
=________.
“a≥0”是“∃x∈R,ax2+x+1≥0为真命题”的________条件.
曲线 在点(1,2)处切线的斜率为__________.
在点(1,2)处切线的斜率为__________.
【原创】函数 在区间
在区间 恰有一个极值点,则实数
恰有一个极值点,则实数 的取值范围为 .
的取值范围为 .
若复数 为纯虚数,
为纯虚数, 是虚数单位,则实数
是虚数单位,则实数 的值是 .
的值是 .
【原创】已知复数 满足
满足 (
( 为虚数单位),则
为虚数单位),则 .
.
已知边长分别为a、b、c的三角形ABC面积为S,内切圆O半径为r,连接OA、OB、OC,则三角形OAB、OBC、OAC的面积分别为 cr、
cr、 ar、
ar、 br,由S=
br,由S= cr+
cr+ ar+
ar+ br得r=
br得r= ,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
函数 的定义域为 .
的定义域为 .
【原创】已知函数 对任意的
对任意的 满足
满足 ,且当
,且当 时,
时, .若
.若 有4个零点,则实数
有4个零点,则实数 的取值范围是 .
的取值范围是 .
设函数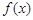 =
=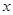 |
|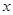 |+b
|+b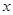 +c,给出下列四个命题:
+c,给出下列四个命题:
①若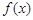 是奇函数,则c=0
是奇函数,则c=0
②b=0时,方程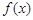 =0有且只有一个实根
=0有且只有一个实根
③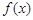 的图象关于(0,c)对称
的图象关于(0,c)对称
④若b 0,方程
0,方程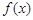 =0必有三个实根
=0必有三个实根
其中正确的命题是 (填序号)
已知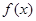 是定义在
是定义在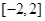 上的函数,且对任意实数
上的函数,且对任意实数 ,恒有
,恒有 ,且
,且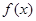 的最大值为1,则不等式
的最大值为1,则不等式 的解为
的解为
 ,则
,则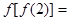 .
.
【原创】若函数 ,则
,则
(1)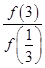 =________.
=________.
(2)f(3)+f(4)+…+f(2 015)+ +
+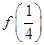 +…+
+…+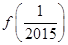 =________.
=________.
已知 ,
, ,
,
(1)求 和
和 ;
;
(2)若记符号 ,
,
①在图中把表示“集合 ”的部分用阴影涂黑;
”的部分用阴影涂黑;
②求 和
和 .
.
已知复数z1=m(m-1)+(m-1)i是纯虚数.
(1)求实数m的值;
(2)若(3+z1) =4+2i,求复数z.
=4+2i,求复数z.
已知 ,求证:关于
,求证:关于 的三个方程
的三个方程 ,
, ,
, 中至少有一个方程有实数根.
中至少有一个方程有实数根.
已知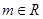 ,命题
,命题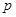 :对任意
:对任意 ,不等式
,不等式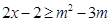 恒成立;命题
恒成立;命题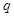 :存在
:存在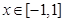 ,使得
,使得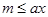 成立
成立
(Ⅰ)若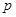 为真命题,求
为真命题,求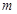 的取值范围;
的取值范围;
(Ⅱ)当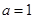 ,若
,若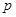 且
且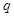 为假,
为假,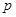 或
或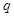 为真,求
为真,求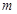 的取值范围。
的取值范围。
(Ⅲ)若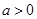 且
且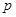 是
是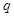 的充分不必要条件,求
的充分不必要条件,求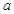 的取值范围。
的取值范围。
已知函数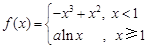 ,其中
,其中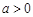
(Ⅰ)求 在
在 上的单调区间;
上的单调区间;
(Ⅱ)求 在
在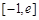 (
(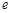 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;
(Ⅲ)对任意给定的正实数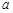 ,曲线
,曲线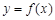 上是否存在两点
上是否存在两点 、
、 ,使得
,使得 是以原点
是以原点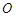 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在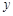 轴上?
轴上?
【原创】设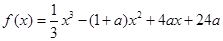 ,其中
,其中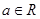 .
.
(1)若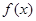 无极值,求
无极值,求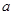 的取值范围;
的取值范围;
(2)若当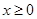 ,
, 恒成立,求
恒成立,求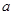 的取值范围.
的取值范围.