已知集合A= -1, 1, 3
-1, 1, 3  ,B=
,B= 3,
3,
 ,且B
,且B A.则实数
A.则实数 的值是______.
的值是______.
【原创】已知复数 ,则
,则 ________.
________.
命题“若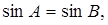 则
则 ”的逆否命题是____________
”的逆否命题是____________
设集合 ,集合
,集合 .若
.若 ,则
,则 _______.
_______.
已知(1+ )2=a+bi(a,b
)2=a+bi(a,b R,i为虚数单位),则a+b= .
R,i为虚数单位),则a+b= .
已知p:(x-1)(y-2)=0,q:(x-1)2+(y-2)2=0,则p是q的________条件
函数 的单调递减区间是____________________.
的单调递减区间是____________________.
直线 与曲线
与曲线 相切,则切点的坐标为 .
相切,则切点的坐标为 .
命题“ ”为假命题,则实数
”为假命题,则实数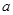 的取值范围为
的取值范围为
若 是奇函数,则
是奇函数,则 的值是_______.
的值是_______.
【原创】若函数 在
在 上递减,则实数
上递减,则实数 的取值范围是__________.
的取值范围是__________.
已知 为
为 上的偶函数,对任意
上的偶函数,对任意 都有
都有 且当
且当 ,
, 时,有
时,有 成立,给出四个命题:①
成立,给出四个命题:① ;②直线
;②直线 是函数
是函数 的图像的一条对称轴;③函数
的图像的一条对称轴;③函数 在
在 上为增函数;④函数
上为增函数;④函数 在
在 上有四个零点,其中所有正确命题的序号为 .
上有四个零点,其中所有正确命题的序号为 .
若 ,则
,则 的最小值是 .
的最小值是 .
【原创】如图是函数 的导函数
的导函数 的图象,给出下列命题
的图象,给出下列命题

 是函数
是函数 的极值点.
的极值点.
② 是函数
是函数 的极大值点.
的极大值点.
③ 在
在 处切线斜率小于
处切线斜率小于 .
.
④ 在区间
在区间 上单调递增.则正确命题的序号是 .
上单调递增.则正确命题的序号是 .
已知集合 ,
, ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
【原创】设命题p:函数 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式 对一切实数均成立.
对一切实数均成立.
(1)如果 p是真命题,求实数
p是真命题,求实数 的取值范围;
的取值范围;
(2)如果命题“p或q”为真命题,且“p且q”为假命题,求实数 的取值范围.
的取值范围.
已知 是复数,若
是复数,若 为实数(
为实数( 为虚数单位),且
为虚数单位),且 为纯虚数.
为纯虚数.
(1)求复数 ;
;
(2)若复数 在复平面上对应的点在第四象限,求实数
在复平面上对应的点在第四象限,求实数 的取值范围
的取值范围
已知a是整数,a2是偶数,求证:a也是偶数.
已知函数 ,
, .
.
(1)若 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)试讨论 的单调区间.
的单调区间.
已知二次函数 ,满足
,满足 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根.
(1)求函数 的解析式;
的解析式;
(2)当
 时,求函数
时,求函数 的最小值
的最小值 的表达式.
的表达式.