已知集合 ,
, ,则
,则
复数 .
.
已知命题p:m∈R,且m+1≤0,命题q:∀x∈R,x2+mx+1>0恒成立,若p∧q为假命题,则m的取值范围是________.
已知集合 ,则集合A的子集个数为_______.
,则集合A的子集个数为_______.
已知复数 ,且
,且 是实数,则实数k= .
是实数,则实数k= .
已知p:(x-1)(y-2)=0,q:(x-1)2+(y-2)2=0,则p是q的________条件
已知函数 ,若函数
,若函数 的零点所在的区间为
的零点所在的区间为 ,则
,则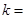 .
.
函数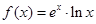 在点
在点 处的切线方程为 .
处的切线方程为 .
【原创】命题“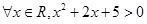 ”的否定是 .
”的否定是 .
已知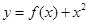 是奇函数,且
是奇函数,且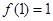 ,若
,若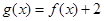 ,则
,则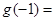 .
.
【原创】函数 的单调增区间为 .
的单调增区间为 .
已知实数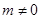 ,函数
,函数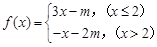 ,若
,若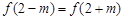 ,则实数
,则实数 的
的
值为 .
【原创】某节课上,有学生列举了如下一些结论:
①函数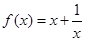 在
在 上有最大值
上有最大值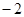 ;
;
②函数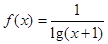 在
在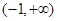 上是减函数;
上是减函数;
③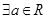 ,使函数
,使函数 为奇函数;
为奇函数;
④对数函数具有性质“对任意实数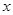 ,
,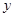 ,满足
,满足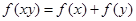 ”
”
⑤指数函数具有性质“对任意实数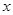 ,
,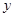 ,满足
,满足 ”
”
其中正确的结论是_______.(填写你认为正确结论的序号)
函数 对于
对于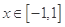 总有
总有
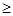 0 成立,则
0 成立,则 = .
= .
已知集合 ,
,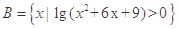 .
.
(Ⅰ)求集合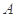 和
和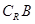 ;
;
(Ⅱ)若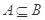 ,求实数
,求实数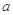 的取值范围.
的取值范围.
已知命题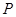 :“若
:“若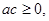 则二次方程
则二次方程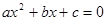 没有实根”.
没有实根”.
(1)写出命题 的否命题;
的否命题;
(2)判断命题 的否命题的真假, 并证明你的结论.
的否命题的真假, 并证明你的结论.
已知 为复数,
为复数,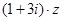 为纯虚数,
为纯虚数,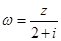 ,且
,且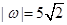 ,求复数
,求复数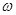 .
.
已知 ,试证明
,试证明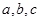 至少有一个不小于1.
至少有一个不小于1.
【原创】已知函数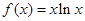 ,
,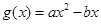 (a、b为常数).
(a、b为常数).
(1)求函数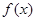 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)当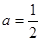 时,设
时,设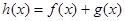 ,若函数
,若函数 在区间
在区间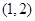 上存在极值点,求实数b的取值范围;
上存在极值点,求实数b的取值范围;
已知函数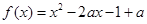 ,
,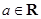 .
.
(Ⅰ)若 ,试求函数
,试求函数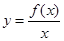 (
( )的最小值;
)的最小值;
(Ⅱ)对于任意的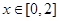 ,不等式
,不等式 成立,试求
成立,试求 的取值范围.
的取值范围.