复数 的共轭复数为
的共轭复数为
 的定义域是 .
的定义域是 .
【原创】已知数列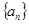 的前
的前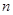 项和为
项和为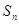 ,若
,若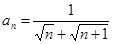 ,
,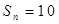 ,则
,则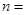 .
.
下列命题中正确的是 .
①若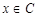 ,则方程
,则方程 只有一个根
只有一个根
②若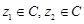 且
且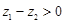 ,则
,则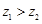
③若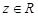 ,则
,则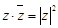 不成立
不成立
④若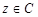 ,且
,且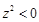 ,那么
,那么 一定是纯虚数
一定是纯虚数
下列表述正确的是( )
①归纳推理是由特殊到一般的推理;
②演绎推理是由一般到特殊的推理;
③类比推理是由特殊到一般的推理;
④分析法是一种间接证明法;
⑤若z∈C,且|z+2﹣2i|=1,则|z﹣2﹣2i|的最小值是3.
【原创】已知函数 的导函数为
的导函数为 ,且满足关系式
,且满足关系式 ,则
,则 的值等于 .
的值等于 .
某展览会一周(七天)内要接待三所学校学生参观,每天只安排一所学校,其中甲学校要连续参观两天,其余学校均参观一天,则不同的安排方法有 种.
函数 满足
满足 ,则
,则 的所有可能值为 .
的所有可能值为 .
【原创】若关于 的不等式
的不等式 对任意实数
对任意实数 恒成立,则
恒成立,则 的最大值为 .
的最大值为 .
在数列 中,若对于任意的
中,若对于任意的 均有
均有 为定值,且
为定值,且 ,
, ,
, ,则数列
,则数列 的前100项的和
的前100项的和 = .
= .
 的展开式中常数项为 .
的展开式中常数项为 .
【原创】已知函数f(x)定义域为D,若∀a,b,c∈D,f(a),f(b),f(c)都是某一三角形的三边,则称f(x)为定义在D上的“保三角形函数”,以下说法正确的是 .
①f(x)=2(x∈R)不是R上的“保三角形函数”
②若定义在R上的函数f(x)的值域为[ ,2],则f(x)一定是R上的“保三角形函数”
,2],则f(x)一定是R上的“保三角形函数”
③f(x)= 是其定义域上的“保三角形函数”
是其定义域上的“保三角形函数”
④当t>1时,函数f(x)=ex+t一定是[0,1]上的“保三角形函数”
【原创】在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:
(1)对任意a∈R,a*0=a;
(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).
则函数f(x)=(ex)* 的最小值为是 .
的最小值为是 .
若函数 在其定义域内的一个子区间
在其定义域内的一个子区间 内不是单调函数,则实数k的取值范围是 .
内不是单调函数,则实数k的取值范围是 .
已知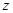 是复数,若
是复数,若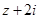 为实数(
为实数(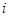 为虚数单位),且
为虚数单位),且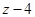 为纯虚数.
为纯虚数.
(1)求复数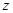 ;
;
(2)若复数 在复平面上对应的点在第四象限,求实数
在复平面上对应的点在第四象限,求实数 的取值范围
的取值范围
已知数列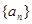 前项和
前项和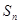 且
且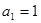 ,
,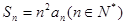
(1)试求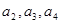
(2)猜想 的表达式,并用数学归纳法证明猜想.
的表达式,并用数学归纳法证明猜想.
用一颗骰子连掷三次,投掷出的数字顺次排成一个三位数,此时:
(1)各位数字互不相同的三位数有多少个?
(2)可以排出多少个不同的数?
(3)恰好有两个相同数字的三位数共有多少个?
正项数列 满足
满足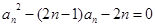 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令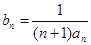 ,求数列
,求数列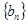 的前
的前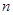 项和
项和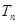 .
.
已知函数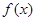 在
在 上满足
上满足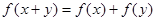 ,且当
,且当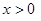 时,
时,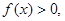
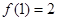 。
。
(1)求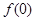 、
、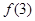 的值;
的值;
(2)判定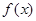 的单调性;
的单调性;
(3)若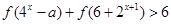 对任意x恒成立,求实数
对任意x恒成立,求实数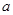 的取值范围。
的取值范围。
【原创】设函数 .
.
(1)若函数 在定义域上为增函数,求实数
在定义域上为增函数,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,若函数 ,
, 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.