【原创】下列命题中正确的是
①若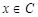 ,则方程
,则方程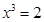 只有一个根
只有一个根
②若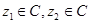 且
且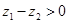 ,则
,则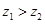
③若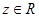 ,则
,则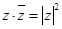 不成立
不成立
④若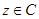 ,且
,且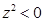 ,那么
,那么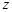 一定是纯虚数
一定是纯虚数
【原创】下列表述正确的是 .
①归纳推理是由特殊到一般的推理;
②演绎推理是由一般到特殊的推理;
③类比推理是由特殊到一般的推理;
④分析法是一种直接证明法;
⑤若z∈C,且|z+2﹣2i|=1,则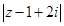 的最小值是4.
的最小值是4.
函数 的零点的个数是
的零点的个数是
若复数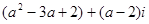 是纯虚数,则实数a的值为 .
是纯虚数,则实数a的值为 .
【原创】数列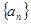 的前
的前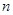 项和记为
项和记为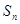 ,若
,若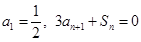 ,
,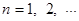 ,则数列
,则数列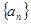 的通项公式为
的通项公式为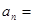 .
.
从1=12 2+3+4=32 3+4+5+6+7=52中,可得到一般规律为 .
若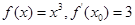 ,则
,则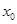 的值为 .
的值为 .
某班级要从4名男生、2名女生中选派4人参加社区服务,如果要求至少有1名女生,那么不同的选派方案种数为 .(用数字作答)
【原创】设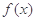 是定义在R上的周期为2的函数,当
是定义在R上的周期为2的函数,当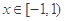 时,
时,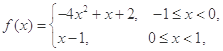 ,则
,则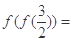 。
。
函数 在点
在点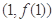 处的切线方程为 .
处的切线方程为 .
已知数列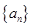 的前n项和
的前n项和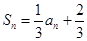 ,则
,则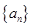 的通项公式
的通项公式
函数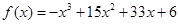 的单调减区间为 .
的单调减区间为 .
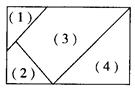
用五种不同的颜色,给图中的(1)(2)(3)(4)的各部分涂色,每部分涂一种颜色,相邻部分涂不同颜色,则涂色的方法共有 种。
对定义在区间D上的函数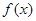 和
和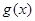 ,如果对任意
,如果对任意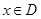 ,都有
,都有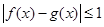 成立,那么称函数
成立,那么称函数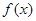 在区间D上可被
在区间D上可被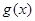 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
①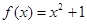 在区间
在区间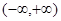 上可被
上可被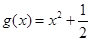 替代;
替代;
②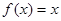 可被
可被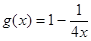 替代的一个“替代区间”为
替代的一个“替代区间”为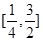 ;
;
③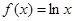 在区间
在区间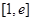 可被
可被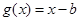 替代,则
替代,则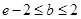 ;
;
④ ,则存在实数
,则存在实数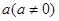 ,使得
,使得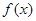 在区间
在区间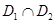 上被
上被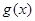 替代;
替代;
其中真命题的有
已知复数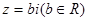 ,
,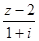 是实数,
是实数,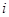 是虚数单位.
是虚数单位.
(1)求复数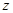 ;
;
(2)若复数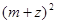 所表示的点在第一象限,求实数
所表示的点在第一象限,求实数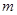 的取值范围.
的取值范围.
设数列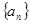 的前
的前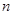 项和为
项和为 ,且
,且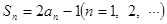 .
.
(1)求数列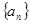 的通项公式;
的通项公式;
(2)若数列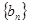 满足
满足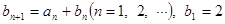 ,求数列
,求数列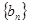 的通项公式.
的通项公式.
对于任意正整数n,猜想2n﹣1与(n+1)2的大小关系,并给出证明.
函数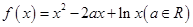 .
.
(1)函数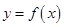 在点
在点 处的切线与直线
处的切线与直线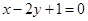 垂直,求a的值;
垂直,求a的值;
(2)讨论函数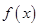 的单调性;
的单调性;
(3)不等式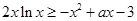 在区间
在区间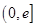 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
【原创】六个人站成一排,求在下列条件下的不同排法种数:
(1)甲必须在排头;
(2)甲、乙相邻;
(3)甲不在排头,并且乙不在排尾;
(4)其中甲、乙两人自左向右从高到矮排列且互不相邻.
已知函数 为奇函数.
为奇函数.
(Ⅰ)若 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)当 时,不等式
时,不等式 在
在 上恒成立,求实数
上恒成立,求实数 的最小值;
的最小值;
(Ⅲ)当 时,求证:函数
时,求证:函数 在
在 上至多一个零点.
上至多一个零点.