已知全集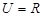 ,
,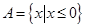 ,
,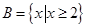 ,则集合
,则集合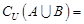 .
.
函数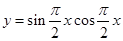 的最小正周期是 .
的最小正周期是 .
已知向量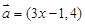 与
与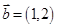 共线,则实数
共线,则实数 的值为
的值为
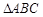 中,角
中,角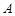 ,
,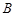 的对边分别为
的对边分别为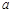 ,
,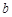 ,则“
,则“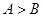 ”是“
”是“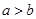 ”的 条件(填“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”).
”的 条件(填“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”).
已知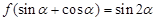 ,则
,则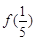 的值为 .
的值为 .
设曲线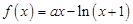 在点
在点 处的切线方程为
处的切线方程为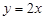 ,则实数
,则实数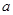 的值为 .
的值为 .
已知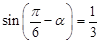 ,则
,则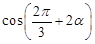 的值是 .
的值是 .
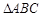 中,
中,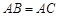 ,
, 的边长为
的边长为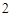 ,则
,则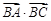 的值为 .
的值为 .
若将函数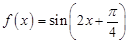 的图像向右平移
的图像向右平移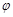 个单位,所得图像关于
个单位,所得图像关于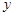 轴对称,则
轴对称,则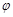 的最小正值是 .
的最小正值是 .
若 ,则
,则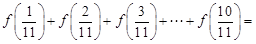
函数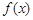 是定义在
是定义在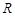 上的奇函数,
上的奇函数,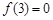 ,且
,且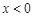 时,
时,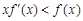 ,则不等式
,则不等式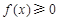 的解集是 .
的解集是 .
如图,△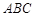 中,延长
中,延长 到
到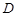 ,使
,使 ,当
,当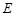 点在线段
点在线段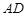 上移动时,若
上移动时,若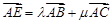 ,则
,则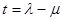 的最大值是 .
的最大值是 .
已知函数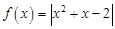 ,
,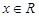 .若方程
.若方程 恰有4个互异的实数根,则实数
恰有4个互异的实数根,则实数 的取值范围为 .
的取值范围为 .
若函数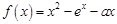 在
在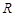 上存在单调递增区间,则实数
上存在单调递增区间,则实数 的取值范围是 .
的取值范围是 .
(本小题满分14分)在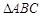 中,内角
中,内角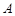 ,
,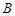 ,
,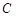 的对边分别为
的对边分别为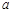 ,
,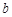 ,
,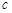 ,且
,且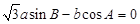 .
.
(1)求角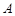 的大小;
的大小;
(2)若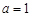 ,
,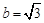 ,求
,求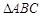 的面积.
的面积.
已知函数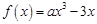 .
.
(1)求函数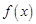 单调区间;
单调区间;
(2)若在区间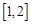 上,
上,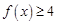 恒成立,求实数
恒成立,求实数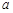 的取值范围.
的取值范围.
(本小题满分14分)某实验室某一天的温度(单位: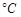 )随时间t(单位:h)的变化近似满足函数关系:
)随时间t(单位:h)的变化近似满足函数关系: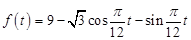 ,
,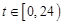 .
.
(1)求实验室这一天里,温度降低的时间段;
(2)若要求实验室温度不高于10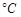 ,则在哪段时间实验室需要降温?
,则在哪段时间实验室需要降温?
如图,在平面直角坐标系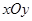 中,已知四边形
中,已知四边形 是等腰梯形,
是等腰梯形,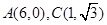 ,点
,点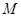 满足
满足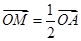 ,点
,点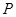 在线段
在线段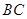 上运动(包括端点).
上运动(包括端点).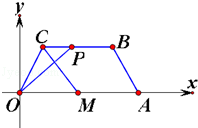
(1)求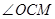 的余弦值;
的余弦值;
(2)是否存在实数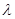 ,使
,使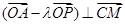 ,若存在,求出满足条件的实数
,若存在,求出满足条件的实数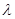 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(本小题满分16分)已知函数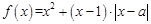 .
.
(1)若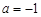 ,解方程
,解方程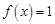 ;
;
(2)若函数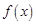 在
在 上单调递增,求实数
上单调递增,求实数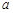 的取值范围;
的取值范围;
(3)若函数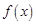 在
在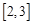 上的最小值为6,求实数
上的最小值为6,求实数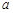 的值.
的值.
(本小题满分16分)已知函数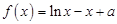 有且只有一个零点,其中a>0.
有且只有一个零点,其中a>0.
(1)求a的值;
(2)若对任意的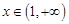 ,有
,有 恒成立,求实数k的最小值;
恒成立,求实数k的最小值;
(3)设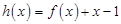 ,对任意
,对任意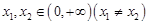 ,
,
证明:不等式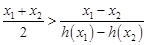 恒成立.
恒成立.