设 ,
, 是实数,若
是实数,若 (
( 是虚数单位),则
是虚数单位),则 的值是 .
的值是 .
已知集合 ,
, ,则
,则 = .
= .
平行四边形 中,
中, 为
为 的中点.若在平行四边形
的中点.若在平行四边形 内部随机取一点
内部随机取一点 ,则点
,则点 取自
取自 内部的概率为 .
内部的概率为 .
为了解某地区高三学生的身体发育情况,抽查了该地区 名高三男生的体重. 根据抽样测量后的男生体重(单位:
名高三男生的体重. 根据抽样测量后的男生体重(单位: )数据绘制的频率分布直方图如图所示,则这
)数据绘制的频率分布直方图如图所示,则这 名学生中体重值在区间[56.5,64.5)的人数是 .
名学生中体重值在区间[56.5,64.5)的人数是 .
运行如图语句,则输出的结果 .
.
设等比数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则 .
.
若关于 的不等式
的不等式 的解集为
的解集为 ,则实数
,则实数 .
.
在△ABC中,AB=2,AC=1,D为BC的中点,则 = .
= .
已知锐角 ,
, 满足
满足 ,则
,则 的最大值为 .
的最大值为 .
设a>0,集合A={(x,y)| },B={(x,y)|
},B={(x,y)| }.若点P(x,y)∈A是点P(x,y)∈B的必要不充分条件,则a的取值范围是 .
}.若点P(x,y)∈A是点P(x,y)∈B的必要不充分条件,则a的取值范围是 .
已知函数 ,若
,若 , 则实数
, 则实数 的最小值为 .
的最小值为 .
已知命题:“在等差数列 中,若
中,若 ,则
,则 为定值”为真命题,由于印刷问题,括号处的数模糊不清,可推得括号内的数为 .
为定值”为真命题,由于印刷问题,括号处的数模糊不清,可推得括号内的数为 .
已知 若关于
若关于 的方程
的方程 在(0,4)上有两个实数解,则
在(0,4)上有两个实数解,则 的取值范围是 .
的取值范围是 .
记数列{an}的前n项和为Sn,若不等式 对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为 .
对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为 .
(本小题满分14分)已知 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量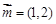 ,
, ,且
,且 .
.
(1)求角A的大小;
(2)若 ,求证:
,求证: 为等边三角形.
为等边三角形.
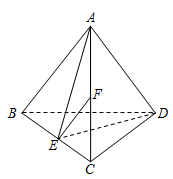
(本小题满分14分)如图,在四面体 中,
中, ,点
,点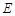 是
是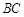 的中点,点
的中点,点 在线段
在线段 上,且
上,且 .
.
(1)若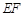 ∥平面
∥平面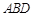 ,求实数
,求实数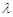 的值;
的值;
(2)求证:平面 平面
平面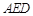 .
.
(本小题满分14分)已知数列{an}是等差数列,{bn}是等比数列,且满足a1+a2+a3=9,b1b2b3=27.若a4=b3,b4-b3=m.
(1)当m=18时,求数列{an}和{bn}的通项公式;
(2)若数列{bn}是唯一的,求m的值.
(本小题满分16分)如图,等腰梯形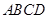 的三边
的三边 分别与函数
分别与函数 ,
, 的图象切于点
的图象切于点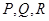 .求梯形
.求梯形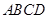 面积的最小值.
面积的最小值.
(本小题16分)已知数列 的各项均为正数,数列
的各项均为正数,数列 ,
, 满足
满足 ,
, .
.
(1)若数列 为等比数列,求证:数列
为等比数列,求证:数列 为等比数列;
为等比数列;
(2)若数列 为等比数列,且
为等比数列,且 ,求证:数列
,求证:数列 为等比数列.
为等比数列.
已知实数 ,函数
,函数 .
.
(1)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若当 时,函数
时,函数 图象上的点均在不等式
图象上的点均在不等式 ,所表示的平面区域内,求实数
,所表示的平面区域内,求实数 的取值范围.
的取值范围.