若集合 ,
, ,则集合
,则集合 .
.
若 ,则
,则 .
.
命题 :“若
:“若 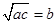 ,则
,则 成等比数列”,则命题
成等比数列”,则命题 的否命题是 (填“真”或“假”之一)命题.
的否命题是 (填“真”或“假”之一)命题.
如果 ,与
,与 是共轭复数(x、y是实数),则
是共轭复数(x、y是实数),则 .
.
在等差数列 中,
中, 则
则 .
.
已知 三点的坐标分别为
三点的坐标分别为 ,且
,且 在线段
在线段 上,
上, ,则
,则 的最大值为 .
的最大值为 .
已知 ,设
,设 为数列
为数列 的最大项,则
的最大项,则 .
.
已知实数 ,函数
,函数 ,若
,若 ,则
,则 = .
= .
函数 的图象与
的图象与 的图象所有交点的横坐标之和等于 .
的图象所有交点的横坐标之和等于 .
已知 是
是 的中线,若
的中线,若 ,
, ,则
,则 的最小值是 .
的最小值是 .
如图, 是同一平面内的三条平行直线,
是同一平面内的三条平行直线, 与
与 间的距离是1,
间的距离是1, 与
与 间的距离是2,正三角形
间的距离是2,正三角形 的三顶点分别在
的三顶点分别在 上,则
上,则 的边长是 .
的边长是 .
将函数 的图象,向左平移
的图象,向左平移 个单位,得到
个单位,得到 函数的图象.若
函数的图象.若 在
在 上为增函数,则
上为增函数,则 的最大值为 .
的最大值为 .
定义 是
是 上的奇函数,且当
上的奇函数,且当 时,
时, .若对任意的
.若对任意的 均有
均有 ,则实数
,则实数 的取值范围为 .
的取值范围为 .
对任意的 ,总有
,总有  ,则
,则 的取值范围是 .
的取值范围是 .
(本小题满分14分)设集合 ,
, .
.
(1)若 ,求实数
,求实数 的值;
的值;
(2)求 ,
, .
.
已知函数
(1)将 写成
写成 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(2)如果 的三边
的三边 满足
满足 ,且边
,且边 所对的角为
所对的角为 ,试求
,试求 的范围及此时函数
的范围及此时函数 的值域.
的值域.
已知扇形 的半径等于1,
的半径等于1, ,
, 是圆弧
是圆弧 上的一点.
上的一点.
(1)若 ,求
,求 的值.
的值.
(2)若 ,①求
,①求 满足的条件;②求
满足的条件;②求 的取值范围.
的取值范围.
(本小题满分15分)为合理用电缓解电力紧张,某市将试行“峰谷电价”计费方法,在高峰用电时段,即居民户每日8时至22时,电价每千瓦时为0.56元,其余时段电价每千瓦时为0.28元.而目前没有实行“峰谷电价”的居民用户电价为每千瓦时为0.53元.若总用电量为 千瓦时,设高峰时段用电量为
千瓦时,设高峰时段用电量为 千瓦时.
千瓦时.
(1)写出实行峰谷电价的电费 及现行电价的电费的
及现行电价的电费的 函数解析式及电费总差额
函数解析式及电费总差额 的解析式;
的解析式;
(2)对于用电量按时均等的电器(在全天任何相同长的时间内,用电量相同),采用峰谷电价的计费方法后是否能省钱?说明你的理由.
(本小题满分16分)已知数列 、
、 ,其中,
,其中, ,数列
,数列 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)是否存在自然数 ,使得对于任意
,使得对于任意 有
有 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;
的最小值;
(3)若数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分16分)已知函数 (
( 是不同时为零的常数),导函数为
是不同时为零的常数),导函数为 .
.
(1)当 时,若存在
时,若存在 ,使得
,使得 成立,求
成立,求 的取值范围;
的取值范围;
(2)求证:函数 在
在 内至少有一个零点;
内至少有一个零点;
(3)若函数 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线 ,关于
,关于 的方程
的方程 ,在
,在 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数 的取值范围.
的取值范围.