计算
之值为何？（ ）
| A．0 |
| B．25 |
| C．50 |
| D．80 |
估计
的运算结果应在（ ）
| A．6到7之间 |
| B．7到8之间 |
| C．8到9之间 |
| D．9到10之间 |
已知a+b=
﹣1，ab=﹣1，则a2+ab+b2的值是（ ）
| A．2﹣ |
| B．3﹣ |
| C．2﹣2 |
| D．4﹣2 |
下列计算中，正确的是（ ）
A． |
B． |
C． |
D． |
下列各式中计算正确的是（ ）
A． |
B． |
C． |
D． |
已知a=
+2，b=-2，则
的值为（ ）
A． |
B． |
C． |
D． |
设S=
，则与S最接近的整数是（ ）
| A．2005 |
| B．2006 |
| C．2007 |
| D．2008 |
如果一个三角形的三边长分别为1、k、4．则化简|2k﹣5|﹣
的结果是（ ）
| A．3k﹣11 |
| B．k+1 |
| C．1 |
| D．11﹣3k |
以下计算正确的是（ ）
A． |
B． |
C． |
D． |
若
，计算
的结果是（ ）
| A．X |
B． |
| C．3 |
D． |
三角形的一边长是
cm，这边上的高是
cm，则这个三角形的面积是（ ）
A．3 cm2 |
| B．3cm2 |
C． cm2 |
D． cm2 |
已知△ABC的三边分别为x、y、z．
（1）以
、
、
为三边的三角形一定存在；
（2）以x2、y2、z2为三边的三角形一定存在；
（3）以
（x+y）、（y+z）、（z+x）为三边的三角形一定存在；
（4）以|x﹣y|+l、|y﹣z|+l、|z﹣x|+l为三边的三角形一定存在．
以上四个结论中，正确结论的个数为（ ）
| A．1 |
| B．2 |
| C．3 |
| D．4 |
已知1＜x＜2，
，则
的值是______．
当x=
时，二次根式
=______．
在正方形ABCD中，E是边BC上一点，如果这个正方形的面积为m，△ABE的面积等于正方形面积的四分之一，那么BE的长用含m的代数式表示为______．
已知：
，则
可用含x的有理系数三次多项式来表示为：=____________．
计算（
﹣
）×
的结果是______．
（2+
）2006（2﹣）2005=______．
计算（1+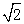
）2011（1﹣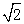）2012=______．
求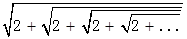
=______．
若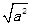
=3，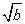
=2，且ab＜0，则a﹣b=______．若
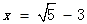，则
的值为______．
已知长方形的面积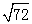为
，一边长为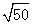
，则另一边长为______．
化简：（
+1）2010•（﹣1）2011=______．
已知m，n是有理数，且（
+2）m+（3﹣2）n+7=0，则m=______，n=______．
（1）﹣72+2×（﹣3）2+（﹣6）÷（﹣
）2（2）2
﹣6
﹣（
）﹣1．
（1）先算乘方，72=49，（﹣3）2=9，
=
，再算乘法和除法，最后合并即可；
（2）先把根式化成最简二次根式，同时求出
=2，再合并同类二次根式即可．
计算：﹣22﹣（﹣3）﹣1﹣
÷
．
计算：6
（
﹣
）
（1）计算：
；
（2）解方程：
计算： 
计算（2
+
）（2﹣）﹣