【原创】若集合 ,集合
,集合 ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
【改编】某校三个年级共有24个班,学校为了了解同学们的心理状况,将每个班编号,依次为l到24,现用系统抽样方法,抽取4个班进行调查,若抽到最后一个编号为21,则抽到的最小编号为( )
| A.2 | B.3 | C.4 | D.5 |
【改编】函数 的部分图像如图示,则将
的部分图像如图示,则将 的图像向右平移
的图像向右平移 个单位后为奇函数,则
个单位后为奇函数,则 的一个值为( )
的一个值为( )

A.  |
B. |
C. |
D. |
一个几何体的三视图如图所示,则这个几何体的外接球的体积为( )

A. |
B. π π |
| C.2π | D. |
设 、
、 R,且
R,且 ,则( )
,则( )
A. |
B. |
C. |
D. |
程序框图如图所示,若其输出结果是140,则判断框中填写的是( )

A. |
B. |
C. |
D. |
已知 为偶函数,当
为偶函数,当 时,
时, ,则不等式
,则不等式 的解集为( )
的解集为( )
A. |
B. |
C. |
D. |
【改编】在 中,内角
中,内角 ,
, ,
, 所对应的边分别为
所对应的边分别为 ,
, ,
, ,若
,若 ,则
,则 的最大值为( )
的最大值为( )
A. |
B. |
C.2 | D.4 |
抛物线 的焦点与双曲线
的焦点与双曲线 的右焦点的连线交
的右焦点的连线交 于第一象限的点M,若
于第一象限的点M,若 在点M处的切线平行于
在点M处的切线平行于 的一条渐近线,则
的一条渐近线,则 ( )
( )
A. |
B. |
C. |
D. |
设函数 (
( ,
, 为自然对数的底数)。若存在
为自然对数的底数)。若存在 使
使 成立,则
成立,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知复数 满足
满足 为虚数单位
为虚数单位 ,则
,则 的模为 .
的模为 .
在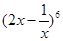 展开式中,常数项等于 .
展开式中,常数项等于 .
【原创】已知函数 ,若
,若 ,则
,则 .
.
如图所示,在边长为2的正六边形 中,动圆
中,动圆 的半径为1,圆心在线段
的半径为1,圆心在线段 (含端点)上运动,
(含端点)上运动, 是圆
是圆 上及内部的动点,设向量
上及内部的动点,设向量 为实数),则
为实数),则 的最大值为____________.
的最大值为____________.
已知函数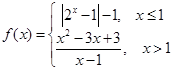 ,下列关于函数
,下列关于函数 (其中a为常数)的叙述中:
(其中a为常数)的叙述中:
①对 a∈R,函数g(x)至少有一个零点;
a∈R,函数g(x)至少有一个零点;
②当a=0时,函数g(x)有两个不同零点;
③ a∈R,使得函数g(x)有三个不同零点;
a∈R,使得函数g(x)有三个不同零点;
④函数g(x)有四个不同零点的充要条件是a<0.
其中真命题有________.(把你认为的真命题的序号都填上)
【改编】(本小题满分12分)在 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足
(1)求角 的值;
的值;
(2)若 且
且 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)下图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
(Ⅰ)求该专业毕业总人数N和90~95分数段内的人数 ;
;
(Ⅱ)现欲将90~95分数段内的 名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为
名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为 ,求
,求 名毕业生中男女各几人(男女人数均至少两人)?
名毕业生中男女各几人(男女人数均至少两人)?
(Ⅲ)在(Ⅱ)的结论下,设随机变量 表示n名毕业生中分配往乙学校的三名学生中男生的人数,求
表示n名毕业生中分配往乙学校的三名学生中男生的人数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知在数列 中,
中, ,
, ,
, .
.
(1)证明数列 是等差数列,并求
是等差数列,并求 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
(本小题满分12分)如图, 垂直于梯形
垂直于梯形 所在的平面,
所在的平面, .
. 为
为 中点,
中点, ,
, 四边形
四边形 为矩形,线段
为矩形,线段 交
交 于点N .
于点N .

(1)求证: // 平面
// 平面 ;
;
(2)求二面角 的大小;
的大小;
(3)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 与平面
与平面 所成角的大小为
所成角的大小为 ? 若存在,请求出
? 若存在,请求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(本小题满分13分)已知椭圆 的离心率为
的离心率为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,设 ,满足
,满足 .
.
(ⅰ)试证 的值为定值,并求出此定值;
的值为定值,并求出此定值;
(ⅱ)试求四边形ABCD面积的最大值.
对于函数 ,若
,若 时,恒有
时,恒有 成立,则称函数
成立,则称函数 是
是 上 的“
上 的“ 函数”.
函数”.
(Ⅰ)当函数 是定义域上的“
是定义域上的“ 函数”时,求实数
函数”时,求实数 的取值范围;
的取值范围;
(Ⅱ)若函数 为
为 上的“
上的“ 函数”.
函数”.
(ⅰ)试比较 与
与 的大小(其中
的大小(其中 );
);
(ⅱ)求证:对于任意大于 的实数
的实数 ,
, ,
, ,,
,, 均有
均有 .
.