己知集合  ,则
,则  中元素的个数为_______.
中元素的个数为_______.
设复数z满足  (i是虚数单位),则z的虚部为_______.
(i是虚数单位),则z的虚部为_______.
设向量 ,
, ,则“
,则“ ”是“
”是“ ”成立的 条件 (选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”) .
”成立的 条件 (选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”) .
运行如图所示的程序后,输出的结果为 .

现有5道试题,其中甲类试题2道,乙类试题3道,现从中随机取2道试题,则至少有1道试题是乙类试题的概率为 .
已知样本6,7,8,9,m的平均数是8,则标准差是
以抛物线 的焦点为顶点,顶点为中心,离心率为2的双曲线标准方程为 .
的焦点为顶点,顶点为中心,离心率为2的双曲线标准方程为 .
已知 ,则
,则 =
=
已知函数
 ,则函数
,则函数 的值域为 .
的值域为 .
已知菱形 的边长为
的边长为 ,
, ,点
,点 分别在边
分别在边 上,
上, .若
.若 ,则
,则
已知直线 经过点
经过点 ,则
,则 的取值范围为 .
的取值范围为 .
已知数列 的首项
的首项 ,前
,前 项和为
项和为 ,且满足
,且满足 ,则满足
,则满足 的
的 的最大值为
的最大值为
设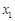 为曲线
为曲线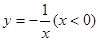 与
与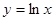 公切线的一个切点横坐标,且
公切线的一个切点横坐标,且 ,则满足
,则满足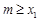 的最小整数
的最小整数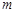 值为 .
值为 .
已知函数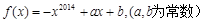 ,若
,若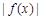 在
在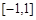 上最小值为
上最小值为 ,则
,则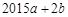 的值为 .
的值为 .
(本小题满分14分)在△ABC中,角A,B,C的对边分别为a,b,c.已知 ,
, .
.
(1)求 的值;
的值;
(2)求 的值;
的值;
(3)若 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分14分)如图,在三棱锥P- ABC中,已知平面PBC  平面ABC.
平面ABC.

(1)若AB  BC,CP
BC,CP PB,求证:CP
PB,求证:CP  PA:
PA:
(2)若过点A作直线 ⊥平面ABC,求证:
⊥平面ABC,求证: //平面PBC.
//平面PBC.
如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为 的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20000元,问如何围可使竹篱笆用料最省?
(本小题满分15分)已知椭圆 的右焦点
的右焦点 ,离心率为
,离心率为 ,过
,过 作两条互相垂直的弦
作两条互相垂直的弦 ,设
,设 的中点分别为
的中点分别为 .
.
(1)求椭圆的方程;
(2)证明:直线 必过定点,并求出此定点坐标;
必过定点,并求出此定点坐标;
(3)若弦 的斜率均存在,求
的斜率均存在,求 面积的最大值.
面积的最大值.
数列 满足:
满足: .
.
(1)求证:数列 一定不是等比数列;
一定不是等比数列;
(2)若 ,求
,求 最小值.
最小值.
已知函数 ,
, .
.
(1)设 .
.
① 若函数 在
在 处的切线过点
处的切线过点 ,求
,求 的值;
的值;
② 当 时,若函数
时,若函数 在
在 上没有零点,求
上没有零点,求 的取值范围;
的取值范围;
(2)设函数 ,且
,且 ,求证:当
,求证:当 时,
时, .
.
(选修4—1:几何证明选讲)
如图,已知点 为
为 的斜边
的斜边 的延长线上一点,且
的延长线上一点,且 与
与 的外接圆相切,过点
的外接圆相切,过点 作
作 的垂线,垂足为
的垂线,垂足为 ,若
,若 ,
, ,求线段
,求线段 的长.
的长.
(选修4—2:矩阵与变换)
在平面直角坐标系xOy中,设曲线 在矩阵
在矩阵 对应的变换作用下得到曲线
对应的变换作用下得到曲线 ,求曲线
,求曲线 的方程.
的方程.
(选修4-4:坐标系与参数方程)
已知直线 的极坐标方程为
的极坐标方程为 ,圆
,圆 的参数方程为
的参数方程为 为参数).
为参数).
(1)请分别把直线 和圆
和圆 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)求直线 被圆截得的弦长.
被圆截得的弦长.
选修4-5:不等式选讲 (本小题满分10分)
若 ,且
,且 ,求
,求 的最小值.
的最小值.
(本小题满分10分)如图,在长方体 中,
中, ,
, ,
, 与
与 相交于点
相交于点 ,点
,点 在线段
在线段 上(点
上(点 与点
与点 不重合).
不重合).
(1)若异面直线 与
与 所成角的余弦值为
所成角的余弦值为 ,求
,求 的长度;
的长度;
(2)若 ,求平面
,求平面 与平面
与平面 所成角的正弦值.
所成角的正弦值.
定义
求(1)
(2)