【改编】若复数 满足
满足 ,则
,则 在复平面内对应的点位于( )
在复平面内对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知全集 ,
, ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
若某市 所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数是( )
所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数是( )

A. |
B. |
C. |
D. |
【改编】等差数列 的前
的前 项和为
项和为 ,且
,且 ,则
,则 等于( )
等于( )
| A.2015 | B.4031 | C.-4022 | D.4026 |
【原创】已知角 的顶点与原点重合,始边与
的顶点与原点重合,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点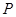 (
( ,
,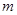 ),且
),且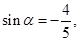 则
则 等于 ( )
等于 ( )
A. |
B. |
C.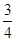 |
D. |
下列叙述中正确的是( )
A.若 为假,则一定是p假q真 为假,则一定是p假q真 |
B.命题“ ”的否定是“ ”的否定是“ ” ” |
C.若a, b,c∈R,则“ ”的充分不必要条件是“a>c” ”的充分不必要条件是“a>c” |
D.设 是一平面,a,b是两条不同的直线,若 是一平面,a,b是两条不同的直线,若 ,则a//b ,则a//b |
如图所示是一个几何体的三视图,则该几何体的表面积为( )

A.4+2 |
B.2+ |
C.2+2 |
D.4+ |
设变量 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
在 中,若
中,若 ,则
,则 是( )
是( )
| A.等边三角形 | B.锐角三角形 | C.钝角三角形 | D.直角三角形 |
【改编】双曲线 上一点
上一点 关于原点的对称点为
关于原点的对称点为 ,
, 为其左焦点,若
为其左焦点,若 ,设
,设 ,则该双曲线的离心率为 ( )
,则该双曲线的离心率为 ( )
A. |
B. |
C. |
D. |
将函数 的图象上各点的横坐标伸长到原的
的图象上各点的横坐标伸长到原的 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移 个单位,所得图象的一条对称轴方程为( )
个单位,所得图象的一条对称轴方程为( )
A. |
B. |
C. |
D. |
已知函数 是定义在R上的增函数,函数
是定义在R上的增函数,函数 的图象关于点
的图象关于点 对称,若任意的
对称,若任意的 ,不等式
,不等式 恒成立,则当
恒成立,则当 时,
时, 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知一个三角形的三边长分别是5,5,6,一只蚂蚁在其内部爬行,若不考虑蚂蚁的大小,则某时刻该蚂蚁距离三角形的三个顶点的距离均超过2的概率是( )
A. |
B. |
C. |
D. |
设 为抛物线
为抛物线
 上一点,
上一点, 为抛物线
为抛物线 的焦点,以
的焦点,以 为圆心、
为圆心、 为半径的圆和抛物线
为半径的圆和抛物线 的准线相交,则
的准线相交,则 的取值范围是 。
的取值范围是 。
如图,为测量坡高MN,选择A和另一个山坡的坡顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知坡高BC=50米,则坡高MN= 米.

若函数 在区间
在区间 上单调递减,则实数t的取值范围是( )
上单调递减,则实数t的取值范围是( )
A. |
B. |
C. |
D. |
已知递增等差数列 中的
中的 是函数
是函数 的两个零点.数列
的两个零点.数列 满足,点
满足,点 在直线
在直线 上,其中
上,其中 是数列
是数列 的前
的前 项和.
项和.
(Ⅰ)求数列 和
和 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列 的前n项和
的前n项和 .
.
【原创】(本小题满分12分)在四棱锥 中,底面
中,底面 为菱形,
为菱形, =
= ,平面
,平面 ⊥平面
⊥平面 ,
, =
= =
= =2.
=2.
(Ⅰ)求证: ⊥
⊥ ;
;
(Ⅱ)求三棱锥 的高.
的高.
(本小题满分12分)有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:
(Ⅰ)求频率分布直方图中 的值;
的值;
(Ⅱ)分别求出成绩落在 中的学生人数;
中的学生人数;
(Ⅲ)从成绩在 的学生中任选2人,求所选学生的成绩都落在
的学生中任选2人,求所选学生的成绩都落在 中的概率.
中的概率.
【改编】(本小题满分12分)已知椭圆C焦点在x轴上,离心率为 ,且经过点M(1,
,且经过点M(1, ).
).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)斜率不为0直线l过椭圆的右焦点F与椭圆C交于 ,
, 两点,如果点
两点,如果点 关于
关于 轴的对称点为
轴的对称点为 ,判断直线
,判断直线 是否经过
是否经过 轴上的定点,如果经过,求出该定点坐标;如果不经过,说明理由.
轴上的定点,如果经过,求出该定点坐标;如果不经过,说明理由.
(本小题满分12分)已知函数 .
.
(Ⅰ)如果函数 在
在 上单调递减,求
上单调递减,求 的取值范围;
的取值范围;
(Ⅱ)当 时,讨论函数
时,讨论函数 零点的个数.
零点的个数.
如图所示,已知 与⊙
与⊙ 相切,
相切, 为切点,过点
为切点,过点 的割线交圆于
的割线交圆于 两点,弦
两点,弦 ,
, 相交于点
相交于点 ,
, 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求
,求 的长.
的长.
极坐标系的极点为直角坐标系 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同.已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同.已知曲线C的极坐标方程为 ,斜率为
,斜率为 的直线
的直线 交y轴于点
交y轴于点 .
.
(Ⅰ)求C的直角坐标方程, 的参数方程;
的参数方程;
(Ⅱ)直线 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求 .
.
设函数
 的最小值为a.
的最小值为a.
(Ⅰ)求a;
(Ⅱ)已知两个正数m,n满足 ,求
,求 的最小值.
的最小值.