设 ,
, ,其中
,其中 是虚数单位,则
是虚数单位,则 .
.
已知集合 ,
, .若
.若 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
为了了解一片经济林的生长情况,随机测量了其中 株树木的底部周长(单位:
株树木的底部周长(单位: ),所得数据如图.则在这
),所得数据如图.则在这 株树木中,底部周长不小于
株树木中,底部周长不小于 的有 株.
的有 株.
设向量 ,
, ,且
,且 ,若
,若 ,则实数
,则实数 .
.
如图所示的流程图的运行结果是 .
将边长为 的正方形
的正方形 沿对角线
沿对角线 折起,使
折起,使 ,则三棱锥
,则三棱锥 的体积为 .
的体积为 .
设等差数列 的前
的前 项和为
项和为 ,若
,若 ,
, . 当
. 当 取最大值时,
取最大值时, .
.
已知 ,且
,且 ,则
,则 .
.
若在区间 内任取实数
内任取实数 ,在区间
,在区间 内任取实数
内任取实数 ,则直线
,则直线 与圆
与圆 相交的概率为 .
相交的概率为 .
设函数 的值域是
的值域是 ,则实数
,则实数 的取值范围为 .
的取值范围为 .
已知函数 满足:当
满足:当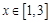 时,
时, ,当
,当 时,
时, .若在区间
.若在区间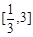
内,函数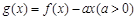 恰有一个零点,则实数
恰有一个零点,则实数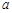 的取值范围是 .
的取值范围是 .
设椭圆 和圆
和圆 ,若椭圆
,若椭圆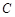 上存在点
上存在点 ,使得过点
,使得过点 引
引
圆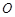 的两条切线,切点分别为
的两条切线,切点分别为 、
、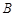 ,满足
,满足 ,则椭圆
,则椭圆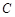 的离心率的取值范围是 .
的离心率的取值范围是 .
设数列 的通项公式为
的通项公式为 ,则满足不等式
,则满足不等式 的正整数
的正整数 的集合为 .
的集合为 .
设函数 ,则满足
,则满足 的
的 的取值范围是 .
的取值范围是 .
(本小题满分14分)在 中,
中, 的对边分别为
的对边分别为 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)设 ,
, 为垂足,若
为垂足,若 ,
, ,求
,求 的值.
的值.
(本小题满分14分)如图,四棱锥 中,底面
中,底面 为矩形,
为矩形, ,
, 为
为 上一点.
上一点.
(1)求证:平面
 平面
平面 ;
;
(2)若 ∥平面
∥平面 ,求证:
,求证: 为
为 的中点.
的中点.
(本小题满分14分)如图,某城市有一条公路从正西方 通过市中心
通过市中心 后转向东偏北
后转向东偏北 角方向的
角方向的 .位于该市的某大学
.位于该市的某大学 与市中心
与市中心 的距离
的距离 ,且
,且 .现要修筑一条铁路L,L在OA上设一站
.现要修筑一条铁路L,L在OA上设一站 ,在OB上设一站B,铁路在
,在OB上设一站B,铁路在 部分为直线段,且经过大学
部分为直线段,且经过大学 .其中
.其中 ,
, ,
, .
.
(1)求大学 与站
与站 的距离
的距离 ;
;
(2)求铁路 段的长
段的长 .
.
(本小题满分16分)设椭圆
 的离心率为
的离心率为 ,直线
,直线 与以原点为圆心、椭圆
与以原点为圆心、椭圆 的短半轴长为半径的圆
的短半轴长为半径的圆 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,以线段
,以线段 为直径作圆
为直径作圆 .若圆
.若圆 与
与 轴相交于不同的两点
轴相交于不同的两点 ,求
,求 的面积;
的面积;
(3)如图, 、
、 、
、 、
、 是椭圆
是椭圆 的顶点,
的顶点, 是椭圆
是椭圆 上除顶点外的任意点,直线
上除顶点外的任意点,直线 交
交 轴于点
轴于点 ,直线
,直线 交
交 于点
于点 .设
.设 的斜率为
的斜率为 ,
, 的斜率为
的斜率为 ,求证:
,求证: 为定值.
为定值.
(本小题满分16分)已知函数 ,
, ,其中函数
,其中函数 的图象在点
的图象在点 处的切线平行于
处的切线平行于 轴.
轴.
(1)确定 与
与 的关系;
的关系;
(2)若 ,试讨论函数
,试讨论函数 的单调性;
的单调性;
(3)设斜率为 的直线与函数
的直线与函数 的图象交于两点
的图象交于两点
 ,求证:
,求证: .
.
(本小题满分16分)设数列 的前
的前 项和为
项和为 ,满足
,满足
 .
.
(1)当 时,
时,
①设 ,若
,若 ,
, .求实数
.求实数 的值,并判定数列
的值,并判定数列 是否为等比数列;
是否为等比数列;
②若数列 是等差数列,求
是等差数列,求 的值;
的值;
(2)当 时,若数列
时,若数列 是等差数列,
是等差数列, ,且
,且 ,
, ,
,
求实数 的取值范围.
的取值范围.
(选修4-1:几何证明选讲)
如图,设 、
、 是圆
是圆 的两条弦,直线
的两条弦,直线 是线段
是线段 的垂直平分线.已知
的垂直平分线.已知 ,求线段
,求线段 的长度.
的长度.
(选修4-2:矩阵与变换)
若点 在矩阵
在矩阵 对应变换的作用下得到点
对应变换的作用下得到点 ,求矩阵
,求矩阵 的逆矩阵.
的逆矩阵.
(选修4-4:坐标系与参数方程)
在极坐标系中,设圆 经过点
经过点 ,圆心是直线
,圆心是直线 与极轴的交点,求圆
与极轴的交点,求圆 的
的
极坐标方程.
(选修4-5:不等式选讲)
设 均为正数,
均为正数, .求证:
.求证: .
.
(本小题满分10分)已知数列 满足
满足 ,
, .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设 ,求证:当
,求证:当 ,
, 时,
时, .
.
(本小题满分10分)如图,已知点 ,直线
,直线 ,
, 为平面内的动点,过
为平面内的动点,过 作
作 的垂线,垂足为
的垂线,垂足为 ,且
,且 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设 是
是 上的任意一点,过
上的任意一点,过 作轨迹
作轨迹 的切线,切点为
的切线,切点为 、
、 .
.
①求证: 、
、 、
、 三点的横坐标成等差数列;
三点的横坐标成等差数列;
②若 ,
, ,求
,求 的值.
的值.