下列函数中,既是奇函数又在其定义域上是增函数的是( )
A. |
B. |
C. |
D. |
命题“任意的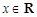 ,都有
,都有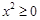 成立”的否定是( )
成立”的否定是( )
A.任意的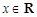 ,都有 ,都有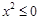 成立 成立 |
B.任意的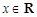 ,都有 ,都有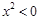 成立 成立 |
C.存在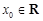 ,使得 ,使得 成立 成立 |
D.存在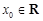 ,使得 ,使得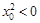 成立 成立 |
要得到函数 的图像,只需将函数
的图像,只需将函数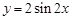 的图象( )
的图象( )
A.向左平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 |
D.向右平移 个单位 个单位 |
若某几何体的三视图(单位: )如图所示,则此几何体的体积是( )
)如图所示,则此几何体的体积是( )
A.  |
B.  |
C.  |
D.  |
若实数 满足不等式组
满足不等式组 ,且
,且 的最小值等于
的最小值等于 ,则实数
,则实数 的值等于( )
的值等于( )
A. |
B. |
C. |
D. |
已知 ,则方程
,则方程 的根的个数是( )
的根的个数是( )
| A.3个 | B.4个 | C.5个 | D.6个 |
在 中,
中, ,
, ,
, 分别为
分别为 的重心和外心,且
的重心和外心,且 ,则
,则 的形状是( )
的形状是( )
| A.锐角三角形 | B.钝角三角形 |
| C.直角三角形 | D.上述三种情况都有可能 |
如图所示, 是双曲线
是双曲线 上的三个点,
上的三个点, 经过原点
经过原点 ,
, 经过右焦点
经过右焦点 ,若
,若 且
且 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. |
B. |
C. |
D. |
集合 ,若
,若 ,则
,则 ;
; ;
;
设两直线 与
与 ,若
,若 ,则
,则 ;若
;若 ,则
,则
已知 为正六边形,若向量
为正六边形,若向量 ,则
,则 ;
; (用坐标表示).
(用坐标表示).
设数列 是公差为
是公差为 的等差数列,若
的等差数列,若 ,则
,则 ;
;
设抛物线 的焦点为
的焦点为 ,
, 为抛物线上一点(在第一象限内),若以
为抛物线上一点(在第一象限内),若以 为直径的圆的圆心在直线
为直径的圆的圆心在直线 上,则此圆的半径为 .
上,则此圆的半径为 .
若实数 满足
满足 ,则
,则 的范围是
的范围是
如图所示的一块长方体木料中,已知 ,设
,设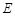 为底面
为底面 的中心,且
的中心,且 ,则该长方体中经过点
,则该长方体中经过点 的截面面积的最小值为 .
的截面面积的最小值为 .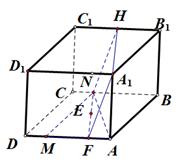
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在
在 上的值域
上的值域
如图所示,在三棱锥 中,
中, ,平面
,平面 ⊥平面
⊥平面 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图所示,椭圆 与直线
与直线 相切于点
相切于点 .
.
(1)求 满足的关系式,并用
满足的关系式,并用 表示点
表示点 的坐标;
的坐标;
(2)设 是椭圆的右焦点,若
是椭圆的右焦点,若 是以
是以 为直角顶点的等腰直角三角形,求椭圆
为直角顶点的等腰直角三角形,求椭圆 的标准方程
的标准方程
已知函数 .
.
(1)若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(2)若对于任意的 ,存在
,存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
已知数列 满足:
满足: ,且
,且 .
.
(1)设 ,求证
,求证 是等比数列;
是等比数列;
(2)(ⅰ)求数列 的通项公式;
的通项公式;
(ⅱ)求证:对于任意 都有
都有 成立
成立