若集合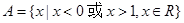 ,
,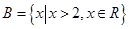 ,则 ( )
,则 ( )
A.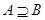 |
B.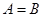 |
C.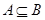 |
D.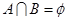 |
已知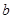 为实数,
为实数,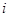 为虚数单位,若
为虚数单位,若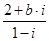 为实数,则
为实数,则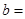 ( )
( )
A.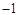 |
B.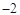 |
C.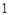 |
D.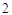 |
下列函数中,既是奇函数又存在极值的函数是 ( )
A.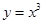 |
B.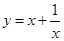 |
C.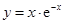 |
D.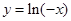 |
若变量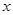 ,
, 满足约束条件
满足约束条件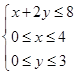 ,则目标函数
,则目标函数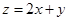 的最大值等于 ( )
的最大值等于 ( )
| A.7 | B.8 | C.10 | D.11 |
在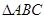 中,
中,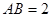 ,
,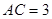 ,
,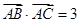 ,则
,则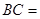 ( )
( )
A.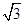 |
B. |
C.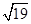 |
D.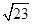 |
下列命题的说法 错误 的是 ( )
A.若复合命题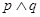 为假命题,则 为假命题,则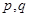 都是假命题. 都是假命题. |
B.“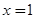 ”是“ ”是“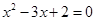 ”的充分不必要条件. ”的充分不必要条件. |
C.对于命题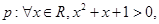 则 则 . . |
D.命题“若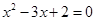 ,则 ,则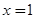 ”的逆否命题为:“若 ”的逆否命题为:“若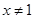 ,则 ,则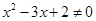 ”. ”. |
多面体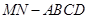 的底面
的底面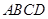 矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则该多面体的体积为 ( )
矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则该多面体的体积为 ( )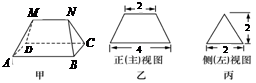
A.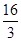 |
B.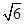 |
C.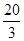 |
D.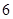 |
对于三次函数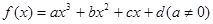 ,给出定义:设
,给出定义:设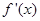 是函数
是函数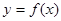 的导数,
的导数,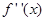 是
是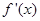 的导数,若方程
的导数,若方程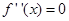 有实数解
有实数解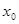 ,则称点
,则称点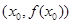 为函数
为函数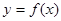 的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心。设函数
的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心。设函数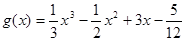 ,则
,则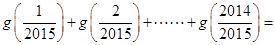 ( )
( )
| A.1 | B.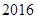 |
C.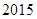 |
D.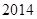 |
设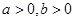 ,若
,若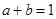 ,则
,则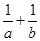 的最小值为__________.
的最小值为__________.
计算积分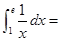 __________.
__________.
某单位为了了解用电量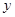 (度)与当天平均气温
(度)与当天平均气温 (°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程
(°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程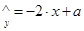 ,则
,则 __________.
__________.
平均气温 (°C) (°C) |
18 |
13 |
10 |
-1 |
用电量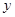 (度) (度) |
25 |
35 |
37 |
63 |
如图所示的程序框图,若输入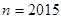 ,则输出的
,则输出的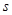 值为__________.
值为__________.
将自然数按如图排列,其中处于从左到右第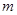 列从下到上第
列从下到上第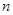 行的数记为
行的数记为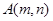 ,
,
如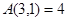 ,
,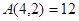 ,则
,则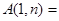 __________;
__________;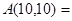 __________.
__________.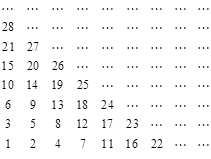
(极坐标与参数方程选做题)若点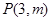 在以点
在以点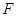 为焦点的抛物线
为焦点的抛物线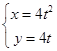 (
(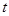 为参数)上,则
为参数)上,则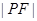 等于______.
等于______.
(几何证明选讲选做题)如图,PA与圆 相切于A,PCB为圆
相切于A,PCB为圆 的割线,并且不过圆心
的割线,并且不过圆心 ,已知
,已知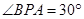 ,
,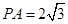 ,
,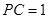 ,则圆
,则圆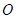 的半径等于__________.
的半径等于__________.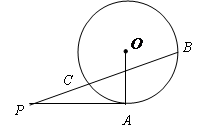
(本小题满分12分)已知函数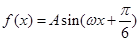
 的最小正周期为
的最小正周期为 ,且
,且 .
.
(1)求 的表达式;
的表达式;
(2)设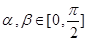 ,
, ,
, ,求
,求 的值.
的值.
(本小题满分12分)一个盒子内装有8张卡片,每张卡片上面写着1个数字,这8个数字各不相同,且奇数有3个,偶数有5个.每张卡片被取出的概率相等.
(1)如果从盒子中一次随机取出2张卡片,并且将取出的2张卡片上的数字相加得到一个新数,求所得新数是奇数的概率;
(2)现从盒子中一次随机取出1张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的数是偶数则停止取出卡片,否则继续取出卡片.设取出了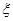 次才停止取出卡片,求
次才停止取出卡片,求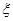 的分布列和数学期望.
的分布列和数学期望.
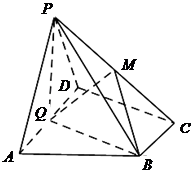
(本小题满分14分)如图,在四棱锥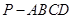 中,底面
中,底面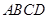 为直角梯形,
为直角梯形,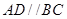 ,
,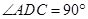 ,平面
,平面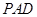 ⊥底面
⊥底面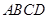 ,
,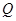 为
为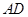 的中点,
的中点,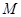 是棱
是棱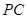 上的点,
上的点,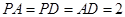 ,
,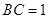 ,
,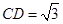 .
.
(1)求证:平面 ⊥平面
⊥平面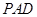 ;
;
(2)若二面角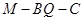 为
为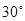 ,设
,设 ,试确定
,试确定 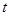 的值.
的值.
(本小题满分14分)已知数列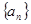 的前
的前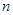 项和为
项和为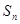 ,
,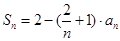 ,
,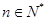 .
.
(1)求数列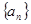 的通项公式;
的通项公式;
(2)设数列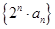 的前
的前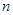 项和为
项和为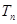 ,
,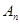 =
=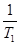 +
+ +
+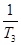 + +
+ + .试比较
.试比较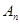 与
与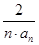 的大小.
的大小.
(本小题满分14分)在直角坐标系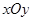 中,曲线
中,曲线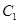 上的点均在圆
上的点均在圆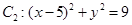 外,且对
外,且对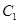 上任意一点
上任意一点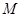 ,
,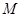 到直线
到直线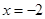 的距离等于该点与圆
的距离等于该点与圆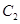 上点的距离的最小值.
上点的距离的最小值.
(1)求曲线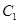 的方程;
的方程;
(2)设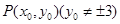 为圆
为圆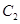 外一点,过
外一点,过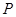 作圆
作圆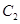 的两条切线,分别与曲线
的两条切线,分别与曲线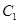 相交于点
相交于点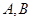 和
和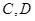 .证明:当
.证明:当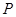 在直线
在直线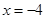 上运动时,四点
上运动时,四点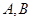
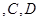 的纵坐标之积为定值.
的纵坐标之积为定值.
(本小题满分14分)已知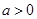 ,函数
,函数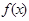 =
=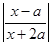 .
.
(1)记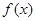 在区间
在区间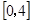 上的最大值为
上的最大值为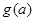 ,求
,求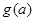 的表达式;
的表达式;
(2)是否存在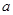 ,使函数
,使函数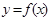 在区间
在区间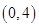 内的图象上存在两点,在该两点处的切线互相垂直?若存在,求
内的图象上存在两点,在该两点处的切线互相垂直?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.