已知集合 ,则
,则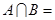 ( )
( )
A.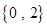 |
B. |
C. |
D. |
若函数 是函数
是函数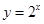 的反函数,则
的反函数,则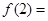 ( )
( )
A.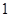 |
B. |
C. |
D. |
已知点 ,
, 和向量a
和向量a ,若a//
,若a// ,则实数
,则实数 的值为 ( )
的值为 ( )
A. |
B. |
C. |
D. |
已知数列 为等差数列,且
为等差数列,且 ,
, ,则
,则 ( )
( )
| A.45 | B.43 | C.40 | D.42 |
下列函数中周期为 且为偶函数的是 ( )
且为偶函数的是 ( )
A. |
B. |
C. |
D. |
已知某几何体的三视图如图所示,则该几何体的体积为 ( )
A. |
B. |
C. |
D. |
已知椭圆与双曲线 的焦点相同,且椭圆上任意一点到两焦点的距离之和为
的焦点相同,且椭圆上任意一点到两焦点的距离之和为 ,那么椭圆的离心率等于 ( )
,那么椭圆的离心率等于 ( )
A. |
B. |
C. |
D. [ [ |
执行如图的程序框图,输出的 = ( )
= ( )
| A.30 | B.25 | C.20 | D.12 |
若变量 ,
, 满足约束条件
满足约束条件 ,则
,则 的最大值等于 ( )
的最大值等于 ( )
A. |
B. |
C.11 | D.10 |
若直角坐标平面内的两个不同点 、
、 满足条件:①
满足条件:① 、
、 都在函数
都在函数 的图像上;②
的图像上;② 、
、 关于原点对称,则称点对
关于原点对称,则称点对 是函数
是函数 的一对“友好点对”(注:点对
的一对“友好点对”(注:点对 与
与 看作同一对“友好点对”).已知函数
看作同一对“友好点对”).已知函数 =
= ,则此函数的“友好点对”有 ( )对.
,则此函数的“友好点对”有 ( )对.
| A.0 | B.1 | C.2 | D.3 |
计算: = .(
= .( 为虚数单位)
为虚数单位)
函数 在
在 处取得极小值.
处取得极小值.
设 ,若
,若 是
是 与
与 的等比中项,则
的等比中项,则 的最小值为 .
的最小值为 .
(坐标系与参数方程选做题)在极坐标系中,圆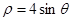 的圆心到直线
的圆心到直线 的
的
距离是 .
(几何证明选做题)如图, 是圆
是圆 的直径,点
的直径,点 在圆
在圆 上,延长
上,延长 到
到 使
使 ,过
,过 作圆
作圆 的切线交
的切线交 于
于 .若
.若 ,
, ,则
,则 .
.
(本小题满分12分)已知函数
 的最小正周期为
的最小正周期为 ,且
,且 .
.
(1)求 的表达式;
的表达式;
(2)设 ,
, ,
, ,求
,求 的值.
的值.
(本小题满分12分)某班 名学生在一次百米测试中,成绩全部介于
名学生在一次百米测试中,成绩全部介于 秒与
秒与 秒之间,将测试结果按如下方式分成五组:第一组
秒之间,将测试结果按如下方式分成五组:第一组 ,第二组
,第二组 , ,第五组
, ,第五组 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
(1)根据频率分布直方图,估计这 名学生百米测试成绩的平均值;
名学生百米测试成绩的平均值;
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于 的概率.
的概率.
(本小题满分14分)
如图所示,在所有棱长都为 的三棱柱
的三棱柱 中,侧棱
中,侧棱 ,
, 点为棱
点为棱 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求四棱锥 的体积.
的体积.
(本小题满分14分)若正项数列 的前
的前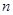 项和为
项和为 ,首项
,首项 ,点
,点 (
(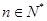 )在曲线
)在曲线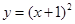 上.源:
上.源:
(1)求数列 的通项公式
的通项公式 ;
;
(2)设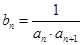 ,
, 表示数列
表示数列 的前
的前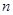 项和,求证:
项和,求证: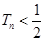 .
.
(本小题满分14分)已知椭圆的中心在原点,焦点在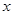 轴上,离心率为
轴上,离心率为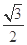 ,且经过点
,且经过点 . 直线
. 直线 交椭圆于不同的两点
交椭圆于不同的两点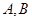 .
.
(1)求椭圆的方程;
(2)求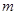 的取值范围;
的取值范围;
(3)若直线 不过点
不过点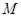 ,求证:直线
,求证:直线 与
与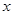 轴围成一个等腰三角形.
轴围成一个等腰三角形.
(本小题满分14分)已知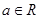 ,函数
,函数 .
.
(1)求 的单调区间;
的单调区间;
(2)证明:当 时,
时,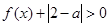 .
.