设 为虚数单位,则复数
为虚数单位,则复数 等于
等于
A. |
B. |
C. |
D. |
平面向量 ,
, ,若
,若 ,则
,则 等于
等于
A. |
B. |
C. |
D. |
下列四个函数中,在闭区间 上单调递增的函数是
上单调递增的函数是
A. |
B. |
C. |
D. |
如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽见解析不计)
A. |
B. |
C. |
D. |
若实数 ,
, 满足约束条件
满足约束条件 ,则
,则 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
如图,在执行程序框图所示的算法时,若输入 ,
, ,
, ,
, 的值依次是
的值依次是 ,
, ,
, ,
, ,
,
则输出 的值为
的值为
A. |
B. |
C. |
D. |
从 ,
, ,
, ,
, ,
, ,
, 这六个数字中任取五个,组成五位数,则不同的五位数共有
这六个数字中任取五个,组成五位数,则不同的五位数共有
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
设 是直角坐标平面上的任意点集,定义
是直角坐标平面上的任意点集,定义 .若
.若 ,则称点集
,则称点集 “关于运算*对称”.给定点集
“关于运算*对称”.给定点集 ,
, ,
, ,其中“关于运算 * 对称”的点集个数为
,其中“关于运算 * 对称”的点集个数为
A. |
B. |
C. |
D. |
不等式 的解集为 .
的解集为 .
已知随机变量 服从正态分布
服从正态分布 ,若
,若 ,
,
则 .
.
已知双曲线的中心在原点,焦点在 轴上,若其渐近线与抛物线
轴上,若其渐近线与抛物线 的准线围成的三角形面积为
的准线围成的三角形面积为 ,则此双曲线的离心率等于 .
,则此双曲线的离心率等于 .
设等差数列 的前
的前 项和为
项和为 ,已知
,已知 ,
, ,则
,则 .
.
已知△ 的内角
的内角 、
、 、
、 所对的边为
所对的边为 、
、 、
、 ,则“
,则“ ”是“
”是“ ”
”
的 条件.(填“充分非必要”、“必要非充分”、“充要”、“既不充分又不必要”中的一种).
(坐标系与参数方程选做题)在直角坐标系中,已知直线 :
: (
( 为参数)与曲线
为参数)与曲线 :
: (
( 为参数)相交于
为参数)相交于 、
、 两点,则
两点,则 _________.
_________.
(几何证明选讲选做题)如图, 、
、 是⊙
是⊙ 的两条切线,切点分别为
的两条切线,切点分别为 、
、 .若
.若 ,
, ,则⊙
,则⊙ 的半径为 .
的半径为 .
(本小题满分12分)设函数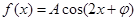 (其中
(其中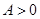 ,
, ,
, ).已知
).已知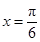 时,
时,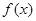 取得最小值
取得最小值 .
.
(1)求函数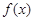 的解析式;
的解析式;
(2)若角 满足
满足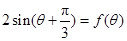 ,且
,且 ,求
,求 的值.
的值.
(本小题满分12分)深圳市于2014年12月29日起实施小汽车限购政策.根据规定,每年发放10万个小汽车名额,其中电动小汽车占20%,通过摇号方式发放,其余名额通过摇号和竞价两种方式各发放一半.政策推出后,某网站针对不同年龄段的申请意向进行了调查,结果如下表所示:
| 申请意向 年龄 |
摇号 |
竞价(人数) |
合计 |
|
| 电动小汽车(人数) |
非电动小汽车(人数) |
|||
| 30岁以下 (含30岁) |
50 |
100 |
50 |
200 |
| 30至50岁 (含50岁) |
50 |
150 |
300 |
500 |
| 50岁以上 |
100 |
150 |
50 |
300 |
| 合计 |
200 |
400 |
400 |
1000 |
(1)采取分层抽样的方式从30至50岁的人中抽取10人,求其中各种意向人数;
(2)在(1)中选出的10个人中随机抽取4人,求其中恰有2人有竞价申请意向的概率;
(3)用样本估计总体,在全体市民中任意选取4人,其中摇号申请电动小汽车意向的人数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
.(本小题满分14分)如图,已知三棱锥 的三条侧棱
的三条侧棱 ,
, ,
, 两两垂直,△
两两垂直,△ 为等边三角形,
为等边三角形,  为△
为△ 内部一点,点
内部一点,点 在
在 的延长线上,且
的延长线上,且 .
.
(1)证明: ;
;
(2)证明:平面 平面
平面 ;
;
(3)若 ,
, ,求二面角
,求二面角 的余弦值.
的余弦值.
(本小题满分14分)设数列 的前
的前 项和为
项和为 ,满足
,满足 ,
, ,且
,且 成等比数列.
成等比数列.
(1)求 ,
, ,
, 的值;
的值;
(2)令 ,求数列
,求数列 的通项公式;
的通项公式;
(3)证明:对一切正整数 ,有
,有
 .
.
(本小题满分14分)已知动点 和定点
和定点 ,
,  的中点为
的中点为 .若直线
.若直线 ,
, 的斜率之积为常数
的斜率之积为常数 (其中
(其中 为原点,
为原点, ),动点
),动点 的轨迹为
的轨迹为 .
.
(1)求曲线 的方程;
的方程;
(2)曲线 上是否存在两点
上是否存在两点 、
、 ,使得△
,使得△ 是以
是以 为顶点的等腰直角三角形?若存在,指出这样的三角形共有几个;若不存在,请说明理由.
为顶点的等腰直角三角形?若存在,指出这样的三角形共有几个;若不存在,请说明理由.
(本小题满分14分)已知函数 ,对任意的
,对任意的 ,满足
,满足 ,其中
,其中 为常数.
为常数.
(1)若 的图像在
的图像在 处切线过点
处切线过点 ,求
,求 的值;
的值;
(2)已知 ,求证:
,求证: ;
;
(3)当 存在三个不同的零点时,求
存在三个不同的零点时,求 的取值范围.
的取值范围.