 是虚数单位,复数
是虚数单位,复数 在复平面内对应的点位于
在复平面内对应的点位于
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
平面向量 ,
, ,若
,若 ,则
,则 等于
等于
A. |
B. |
C. |
D. |
已知集合 ,
, ,则
,则
A. |
B. |
C. |
D. |
命题 ,
, ,则
,则 为
为
A. , , |
B. , , |
C. , , |
D. , , |
已知直线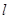 ,平面
,平面 ,则下列能推出
,则下列能推出 的条件是
的条件是
A. , , |
B.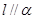 , , |
C.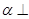  , , |
D.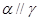 , , |
已知某路口最高限速 ,电子监控测得连续
,电子监控测得连续 辆汽车的速度如图的茎叶图(单位:
辆汽车的速度如图的茎叶图(单位: ).若从中任取
).若从中任取 辆,则恰好有
辆,则恰好有 辆汽车超速的概率为
辆汽车超速的概率为
A. |
B. |
C. |
D. |
.将函数 的图象向右平移
的图象向右平移 个单位,得到的图象关于原点对称,则
个单位,得到的图象关于原点对称,则 的
的
最小正值为
A. |
B. |
C. |
D.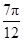 |
.已知双曲线的中心在原点,焦点在 轴上,若其渐近线与圆
轴上,若其渐近线与圆 相切,则
相切,则
此双曲线的离心率等于
A. |
B. |
C. |
D. |
如图所示的程序框图的功能是求 的值,则框图中的①、②两处应
的值,则框图中的①、②两处应
分别填写
A. , , |
B. , , |
C. , , |
D. , , |
定义在 上的函数
上的函数 ,
, 单调递增,
单调递增, ,若对任意
,若对任意 ,存在
,存在 ,
,
使得 成立,则称
成立,则称 是
是 在
在 上的“追逐函数”.已知
上的“追逐函数”.已知 ,下列四个函数:
,下列四个函数:
① ;②
;② ;③
;③ ;④
;④ .其中是
.其中是 在
在 上的“追逐函数”
上的“追逐函数”
的有
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
等差数列 中,
中, ,则
,则 .
.
若实数 满足
满足 ,则
,则 的最小值为 .
的最小值为 .
某几何体的三视图如图所示,其中俯视图为半径为 的四分之一个圆弧,则该几何体的体积为 .
的四分之一个圆弧,则该几何体的体积为 .
(坐标系与参数方程选做题)在直角坐标系中,已知直线 :
: (
( 为参数)与曲线
为参数)与曲线 :
: (
( 为参数)相交于
为参数)相交于 、
、 两点,则
两点,则 _________.
_________.
(几何证明选讲选做题)如图, 、
、 是⊙
是⊙ 的两条切线,切点分别为
的两条切线,切点分别为 、
、 .若
.若 ,
, ,则⊙
,则⊙ 的半径为 .
的半径为 .
(本小题满分12分)在 中,已知
中,已知 ,
, .
.
(1)求 与
与 的值;
的值;
(2)若角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,求
,求 ,
, 的值.
的值.
(本小题满分12分)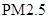 是指空气中直径小于或等于
是指空气中直径小于或等于 微米的颗粒物(也称可入肺颗粒物).为了探究车流量与
微米的颗粒物(也称可入肺颗粒物).为了探究车流量与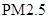 的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与
的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与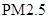 的数据如下表:
的数据如下表:
| 时间 |
周一 |
周二 |
周三 |
周四 |
周五 |
车流量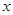 (万辆) (万辆) |
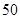 |
 |
 |
 |
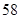 |
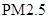 的浓度 的浓度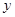 (微克/立方米) (微克/立方米) |
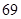 |
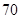 |
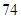 |
 |
 |
(1)根据上表数据,请在下列坐标系中画出散点图;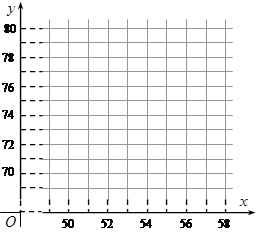
(2)根据上表数据,用最小二乘法求出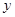 关于
关于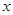 的线性回归方程
的线性回归方程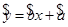 ;
;
(3)若周六同一时间段车流量是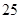 万辆,试根据(2)求出的线性回归方程预测,此时
万辆,试根据(2)求出的线性回归方程预测,此时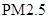 的浓度为多少(保留整数)?
的浓度为多少(保留整数)?
(本小题满分14分)如图, 是边长为
是边长为 的等边三角形,
的等边三角形, 是等腰直角三角形,
是等腰直角三角形, ,平面
,平面
 平面
平面 ,且
,且 平面
平面 ,
, .
.
(1)证明: 平面
平面 ;
;
(2)证明:
 .
.
(本小题满分14分)已知数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, (
( ).
).
(1)求 ,
, 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在整数对 ,使得等式
,使得等式 成立?若存在,请求出所有满足条件的
成立?若存在,请求出所有满足条件的 ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分14分)已知平面上的动点 与点
与点 连线的斜率为
连线的斜率为 ,线段
,线段 的中点与原点连线的斜率为
的中点与原点连线的斜率为 ,
, (
( ),动点
),动点 的轨迹为
的轨迹为 .
.
(1)求曲线 的方程;
的方程;
(2)恰好存在唯一一个同时满足以下条件的圆:
①以曲线 的弦
的弦 为直径;
为直径;
②过点 ;
;
③直径 .求
.求 的取值范围.
的取值范围.
(本小题满分14分)已知函数 ,且对任意
,且对任意 ,都有
,都有 .
.
(1)求 ,
, 的关系式;
的关系式;
(2)若 存在两个极值点
存在两个极值点 ,
, ,且
,且 ,求出
,求出 的取值范围并证明
的取值范围并证明 ;
;
(3)在(2)的条件下,判断 零点的个数,并说明理由.
零点的个数,并说明理由.