已知集合
，
，且
，则实数
的值为 ．
设
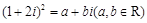，其中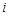
是虚数单位，则
．
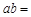已知函数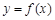
是奇函数，当
时，
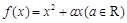，且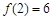
，
则
．
下图是某算法流程图，则程序运行后输出的结果是 ．
设点
，
，
，
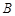是球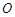
表面上的四个点，
，
，
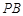两两互相垂直，且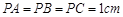
，则球的表面积为 
．
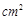已知
，
，若向区域
上随机投掷一点
，则点落入区域
的概率为 ．
将参加夏令营的
名学生编号为：
，采用系统抽样的方法抽取一个容量为
的样本，且随机抽得的号码为
，这名学生分住在三个营区，从
到
在第一营区，从
到
在第二营区，从
到在第三营区，则第三个营区被抽中的人数为 ．
中，“角
成等差数列”是“
”成立的的 条件．
(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”之一)
已知双曲线
，以右顶点为圆心，实半轴长为半径的圆被双曲线的一条
渐近线分为弧长为
的两部分，则双曲线的离心率为 ．
已知
，则
．
已知正数
依次成等比数列，且公比
．将此数列删去一个数后得到的数列(按
原来的顺序)是等差数列，则公比
的取值集合是 ．
如图，梯形
中，
，
，
，若
，则
．
设
的内角
所对的边
成等比数列，则
的取值范围是 ．
设函数
满足
，且当
时，
．若在区间
内，存在
个不同的实数
，使得
，则实数
的取值范围为 ．
（本小题满分14分）在
中，
，
．
（1）求
的值；
（2）若
，求的面积．
（本小题满分14分）如图，在斜三棱柱
中，侧面
是边长为
的菱形，
．在面
中，
，
，
为
的中点，过
三点的平面交
于点
．
（1）求证：为中点；
（2）求证：平面
平面．
（本小题满分14分）某商场为促销要准备一些正三棱锥形状的装饰品，用半径为
的圆形包装纸包装．要求如下：正三棱锥的底面中心与包装纸的圆心重合，包装纸不能裁剪，沿底边向上翻折，其边缘恰好达到三棱锥的顶点，如图所示．设正三棱锥的底面边长为
，体积为
．
（1）求
关于
的函数关系式；
（2）在所有能用这种包装纸包装的正三棱锥装饰品中，的最大值是多少？并求此时的值．
（本小题满分16分）已知椭圆
的离心率为
，并且椭圆经过点
，过原点
的直线
与椭圆
交于
两点，椭圆上一点
满足
．
（1）求椭圆的方程；
（2）证明：
为定值；
（3）是否存在定圆，使得直线绕原点转动时，
恒与该定圆相切，若存在，求出该定圆的方程，若不存在，说明理由．
（本小题满分16分）
已知数列
是等差数列，
是等比数列，且满足
，
．
（1）若
，
．
①当
时，求数列和的通项公式；
②若数列是唯一的，求
的值；
（2）若
，
，
均为正整数，且成等比数列，求数列的公差
的最大值．
（本小题满分16分）设函数
有且仅有两个极值点
．
（1）求实数
的取值范围；
（2）是否存在实数满足
？如存在，求
的极大值；如不存在，请说明理由．
（选修4－1：几何证明选讲）
如图，AD是∠BAC的平分线，圆O过点A且与边BC相切于点D，与边AB、AC分别交于点E、F，求证：EF∥BC．
（选修4－2：矩阵与变换）
已知
，求矩阵
．
（选修4－4：坐标系与参数方程）
在极坐标系中，圆
是以点
为圆心，
为半径的圆．
（1）求圆的极坐标方程；
（2）求圆被直线
所截得的弦长．
（选修4－5：不等式选讲）
设正数
满足
，求
的最小值．
（本小题满分10分）直三棱柱
中，已知
，
，
，
.
是
的中点.
（1）求直线
与平面
所成角的正弦值；
（2）求二面角
的大小的余弦值.
（本小题满分10分）设
且
，集合
的所有
个元素的子集记为
．
（1）求集合中所有元素之和
；
（2）记
为
中最小元素与最大元素之和，求
的值．