已知集合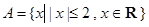 ,
,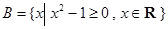 ,则
,则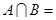 ________.
________.
抛物线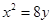 的焦点到准线的距离是______________.
的焦点到准线的距离是______________.
若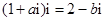 ,其中
,其中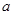 、
、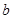
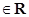 ,
,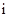 是虚数单位,则
是虚数单位,则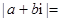 _________.
_________.
已知函数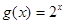 ,若
,若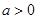 ,
,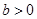 且
且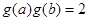 ,则
,则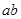 的取值范围是_______.
的取值范围是_______.
设等差数列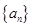 满足
满足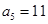 ,
,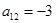 ,
,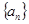 的前
的前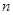 项和
项和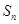 的最大值为
的最大值为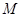 ,则
,则 =__________.
=__________.
若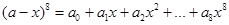 (
(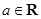 ),且
),且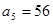 ,则
,则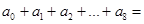 _______________.
_______________.
方程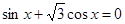 在
在 上的解为_____________.
上的解为_____________.
设变量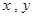 满足约束条件
满足约束条件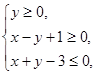 则
则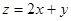 的最大值为_____________.
的最大值为_____________.
若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为__________.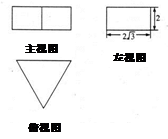
已知定义在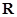 上的单调函数
上的单调函数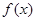 的图像经过点
的图像经过点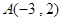 、
、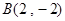 ,若函数
,若函数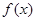 的反函数为
的反函数为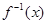 ,则不等式
,则不等式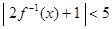 的解集为 .
的解集为 .
现有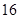 张不同的卡片,其中红色、黄色、蓝色、绿色卡片各
张不同的卡片,其中红色、黄色、蓝色、绿色卡片各 张.从中任取
张.从中任取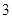 张,要求这
张,要求这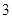 张卡片不能是同一种颜色.则不同取法的种数为____________.
张卡片不能是同一种颜色.则不同取法的种数为____________.
已知函数 ,若
,若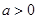 ,关于
,关于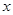 的方程
的方程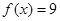 有三个不相等的实数解,则
有三个不相等的实数解,则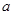 的取值范围是__________.
的取值范围是__________.
在平面直角坐标系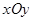 中,点列
中,点列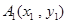 ,
, ,,
,,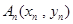 ,,满足
,,满足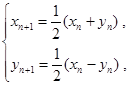 若
若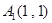 ,则
,则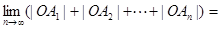 _______.
_______.
把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列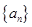 ,若
,若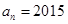 ,则
,则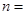 ________.
________.
在△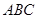 中,“
中,“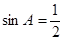 ”是“
”是“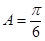 ”的( )
”的( )
| A.充分非必要条件 |
| B.必要非充分条件 |
| C.充要条件 |
| D.既非充分又非必要条件 |
已知平面直角坐标系内的两个向量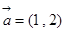 ,
,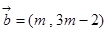 ,且平面内的任一向量
,且平面内的任一向量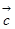 都可以唯一的表示成
都可以唯一的表示成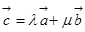
 为实数),则实数
为实数),则实数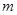 的取值范围是( )
的取值范围是( )
A. |
B.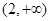 |
C.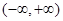 |
D.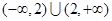 |
设双曲线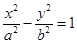 (
(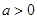 ,
,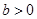 )的虚轴长为
)的虚轴长为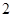 ,焦距为
,焦距为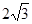 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.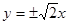 |
B.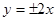 |
C.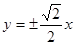 |
D.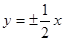 |
在四棱锥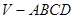 中,
中, ,
,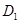 分别为侧棱
分别为侧棱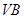 ,
,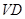 的中点,则四面体
的中点,则四面体 的体积与四棱锥
的体积与四棱锥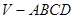 的体积之比为( )
的体积之比为( )
A.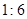 |
B.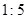 |
C.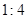 |
D.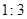 |
本题共有2个小题,第1小题满分6分,第2小题满分6分.
在△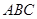 中,已知
中,已知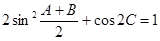 ,外接圆半径
,外接圆半径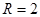 .
.
(1)求角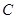 的大小;
的大小;
(2)若角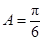 ,求△
,求△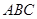 面积的大小.
面积的大小.
本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图,四棱锥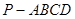 的底面
的底面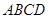 为菱形,
为菱形,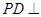 平面
平面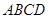 ,
,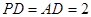 ,
,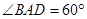 ,
,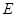 、
、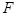 分别为
分别为 、
、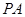 的中点.
的中点.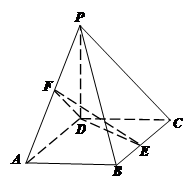
(1)求证: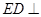 平面
平面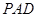 ;
;
(2)求三棱锥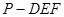 的体积.
的体积.
本题共有2个小题,第1小题满分5分,第2小题满分9分.
某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数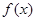 与时刻
与时刻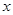 (时)的关系为
(时)的关系为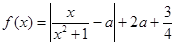 ,
,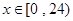 ,其中
,其中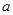 是与气象有关的参数,且
是与气象有关的参数,且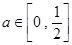 .若用每天
.若用每天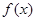 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作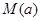 .
.
(1)令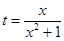 ,
,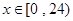 ,求
,求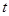 的取值范围;
的取值范围;
(2)求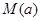 的表达式,并规定当
的表达式,并规定当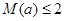 时为综合污染指数不超标,求当
时为综合污染指数不超标,求当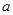 在什么范围内时,该市市中心的综合污染指数不超标.
在什么范围内时,该市市中心的综合污染指数不超标.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知椭圆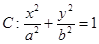 (
(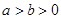 )的焦距为
)的焦距为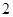 ,且椭圆
,且椭圆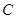 的短轴的一个端点与左、右焦点
的短轴的一个端点与左、右焦点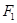 、
、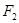 构成等边三角形.
构成等边三角形.
(1)求椭圆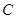 的标准方程;
的标准方程;
(2)设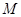 为椭圆上
为椭圆上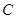 上任意一点,求
上任意一点,求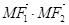 的最大值与最小值;
的最大值与最小值;
(3)试问在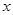 轴上是否存在一点
轴上是否存在一点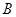 ,使得对于椭圆上任意一点
,使得对于椭圆上任意一点 ,
, 到
到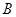 的距离与
的距离与 到直线
到直线 的距离之比为定值.若存在,求出点
的距离之比为定值.若存在,求出点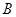 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数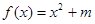 ,其中
,其中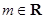 .定义数列
.定义数列 如下:
如下: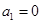 ,
,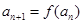 ,
,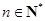 .
.
(1)当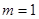 时,求
时,求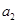 ,
,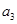 ,
,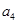 的值;
的值;
(2)是否存在实数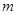 ,使
,使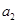 ,
,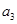 ,
,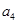 构成公差不为
构成公差不为 的等差数列?若存在,请求出实数
的等差数列?若存在,请求出实数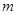 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)求证:当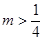 时,总能找到
时,总能找到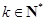 ,使得
,使得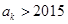 .
.