命题“若
，则
”的逆否命题是（ ）
A．若 ，则 |
B．若，则 |
| C．若，则 |
D．若，则 |
已知
，则下列不等关系式中正确的是（ ）
A． |
B． |
C． |
D． |
已知函数
则
（ ）
A． |
B． |
C． |
D． |
函数
的图象的一部分如图1所示，则此函数的解析
式为（ ）
A． |
B． |
C． |
D． |
已知函数
，若在区间
上任取一个实数
，则使
成立的概
率为（ ）
A． |
B． |
C． |
D． |
如图，圆锥的底面直径
，母线长
，点
在母线
上，且
，有一只蚂蚁沿圆锥的侧面从点
到达点，则这只蚂蚁爬行的最短距离是（ ）
A． |
B． |
C． |
D． |
已知两定点
，
，若直线
上存在点
，使得
，则称直线为“
型直线”．给出下列直线：①
；②
；③
；④
；⑤
．其中是“
型直线”的条数为（ ）
| A．1 | B．2 | C．3 | D．4 |
设
是函数
的图象上一点，向量
，
，且
．
数列
是公差不为0的等差数列，且
，则
（ ）
| A．0 | B．9 | C．18 | D．36 |
已知
为虚数单位，复数
，则
．
执行如图所示的程序框图，则输出的
的值是 ．
已知
，若
，则
．
5名志愿者中安排4人在周六、周日两天参加社区公益活动．若每天安排2人，则不同的安排
方案共有_________种（用数字作答）．
在边长为1的正方形
中，以
为起点，其余顶点为终点的向量分别为
，
，
；以
为起点，其余顶点为终点的向量分别为
，
，
．若
为
的最小值，其中
，
，则
．
（几何证明选讲选做题）如图，在平行四边形
中，
，点
为边
的中点，
与
的延长线交于点
，且平分
，作
，垂足为
，若
，则
的长为 ．
（坐标系与参数方程选做题）在平面直角坐标系中，已知曲线
和
的方程分别为
（
为参数）和
（ 为参数），则曲线和的交点有 个．
（本小题满分12分）已知△
的三边
，
，
所对的角分别为
，
，
，且
．
（1）求
的值；
（2）若△的面积为
，求△外接圆半径的大小．
（本小题满分12分）某市为了宣传环保知识，举办了一次“环保知识知多少”的问卷调查活动（一
人答一份）．现从回收的年龄在20～60岁的问卷中随机抽取了
份，统计结果如下面的图表所示．
| 组号 |
年龄 分组 |
答对全卷 的人数 |
答对全卷的人数 占本组的概率 |
| 1 |
[20,30) |
28 |
 |
| 2 |
[30,40) |
27 |
0．9 |
| 3 |
[40,50) |
5 |
0．5 |
| 4 |
[50,60] |
 |
0．4 |
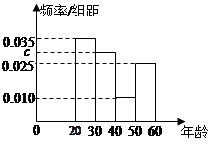
（1）分别求出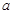
，，
，
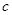的值；
（2）从第3，4组答对全卷的人中用分层抽样的方法抽取6人，在所抽取的6人中随机抽取2人授予“环
保之星”，记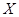
为第3组被授予“环保之星”的人数，求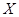的分布列与数学期望．
（本小题满分14分）如图，已知六棱柱
的侧棱垂直于底面，侧棱长与底面边长都为3，
，
分别是棱
，
上的点，且
．
（1）证明：，，
，
四点共面；
（2）求直线
与平面
所成角的正弦值．
（本小题满分14分）已知点
在直线
：
上，
是直线与
轴的
交点，数列
是公差为1的等差数列．
（1）求数列，
的通项公式；
（2）求证：
．
（本小题满分14分）已知圆心在
轴上的圆
过点
和
，圆
的方程为
．
（1）求圆的方程；
（2）由圆上的动点
向圆作两条切线分别交
轴于
，
两点，求
的取值范围．
（本小题满分14分）已知函数
，
（其中
为自然对数的底数）．
（1）若函数
在区间
内是增函数，求实数
的取值范围；
（2）当
时，函数
的图象
上有两点
，
，过点
，
作图象的切线分
别记为
，
，设与的交点为
，证明
．