 的值为( )
的值为( )
A. |
B. |
C. |
D. |
已知函数
 的反函数为
的反函数为 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知双曲线 :
: 经过点
经过点 ,则双曲线
,则双曲线 的离心率为( )
的离心率为( )
A. |
B. |
C. |
D. |
执行如图所示的程序框图,则输出的 的值是( )
的值是( )
A. |
B. |
C. |
D. |
已知命题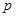 :
: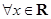 ,
,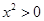 ,命题
,命题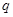 :
: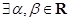 ,使
,使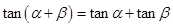 ,则下
,则下
列命题为真命题的是( )
A.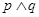 |
B.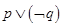 |
C.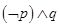 |
D.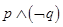 |
设集合 ,
, ,若
,若 ,则实数
,则实数 的取值范围
的取值范围
为( )
A. |
B. |
C. |
D. |
已知数列 满足
满足 ,且
,且
 ,则数列
,则数列 的通项公式为( )
的通项公式为( )
A. |
B. |
C. |
D. |
已知函数 ,若在区间
,若在区间 上任取一个实数
上任取一个实数 ,则使
,则使 成立的概
成立的概
率为( )
A. |
B. |
C. |
D. |
如图,圆锥的底面直径 ,母线长
,母线长 ,点
,点 在母线
在母线 上,且
上,且 ,有一只蚂蚁
,有一只蚂蚁
沿圆锥的侧面从点 到达点
到达点 ,则这只蚂蚁爬行的最短距离是( )
,则这只蚂蚁爬行的最短距离是( )
A. |
B. |
C. |
D. |
设函数 有两个极值点
有两个极值点 ,且
,且 ,
, ,则点
,则点
在 平面上所构成区域的面积为( )
平面上所构成区域的面积为( )
A. |
B. |
C. |
D. |
已知 为虚数单位,复数
为虚数单位,复数 ,则
,则 .
.
已知向量 ,
, ,若
,若 ,则
,则 .
.
某种型号的汽车紧急刹车后滑行的距离
 与刹车时的速度
与刹车时的速度
 的关系可以用
的关系可以用 来描述,已知这种型号的汽车在速度为60
来描述,已知这种型号的汽车在速度为60 时,紧急刹车后滑行的距离为
时,紧急刹车后滑行的距离为
 .一辆这
.一辆这
种型号的汽车紧急刹车后滑行的距离为
 ,则这辆车的行驶速度为
,则这辆车的行驶速度为  .
.
(几何证明选讲选做题)如图,在平行四边形 中,
中, ,点
,点 为边
为边 的中点,
的中点, 与
与 的延长线交于点
的延长线交于点 ,且
,且 平分
平分 ,作
,作 ,垂足为
,垂足为 ,若
,若 ,则
,则 的长为 .
的长为 .
(坐标系与参数方程选做题)在平面直角坐标系中,已知曲线 和
和 的方程分别为
的方程分别为 (
( 为参数)和
为参数)和 (
( 为参数),则曲线
为参数),则曲线 和
和 的交点有 个.
的交点有 个.
(本小题满分12分)已知△ 的三边
的三边 ,
, ,
, 所对的角分别为
所对的角分别为 ,
, ,
, ,且
,且 .
.
(1)求 的值;
的值;
(2)若△ 外接圆的半径为14,求△
外接圆的半径为14,求△ 的面积.
的面积.
(本小题满分12分)某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一
人答一份).现从回收的年龄在20~60岁的问卷中随机抽取了100份,统计结果如下面的图表所示.
| 年龄 分组 |
抽取份数 |
答对全卷 的人数 |
答对全卷的人数 占本组的概率 |
| [20,30) |
40 |
28 |
0.7 |
| [30,40) |
 |
27 |
0.9 |
| [40,50) |
10 |
4 |
 |
| [50,60] |
20 |
 |
0.1 |

(1)分别求出 ,
, ,
, ,
, 的值;
的值;
(2)从年龄在 答对全卷的人中随机抽取2人授予“环保之星”,求年龄在
答对全卷的人中随机抽取2人授予“环保之星”,求年龄在 的人中至少有1
的人中至少有1
人被授予“环保之星”的概率.
(本小题满分14分)如图,已知正方体 的棱长为3,
的棱长为3, ,
, 分别是棱
分别是棱 ,
, 上的点,且
上的点,且 .
.
(1)证明: ,
, ,
, ,
, 四点共面;
四点共面;
(2)平面 将此正方体分为两部分,求这两部分的体积之比.
将此正方体分为两部分,求这两部分的体积之比.
(本小题满分14分)已知点
 在直线
在直线 :
: 上,
上, 是直线
是直线 与
与 轴的
轴的
交点,数列 是公差为1的等差数列.
是公差为1的等差数列.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若 是否存在
是否存在 ,使
,使 成立?若存在,求出所有符合
成立?若存在,求出所有符合
条件的 值;若不存在,请说明理由.
值;若不存在,请说明理由.
(本小题满分14分)已知函数
 .
.
(1)若函数 在
在 处的切线平行于
处的切线平行于 轴,求实数
轴,求实数 的值,并求此时函数
的值,并求此时函数 的极值;
的极值;
(2)求函数 的单调区间.
的单调区间.
(本小题满分14分)已知圆心在 轴上的圆
轴上的圆 过点
过点 和
和 ,圆
,圆 的方程为
的方程为 .
.
(1)求圆 的方程;
的方程;
(2)由圆 上的动点
上的动点 向圆
向圆 作两条切线分别交
作两条切线分别交 轴于
轴于 ,
, 两点,求
两点,求 的取值范围.
的取值范围.