若集合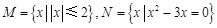 ,则
,则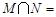 .
.
若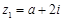 ,
,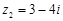 ,且
,且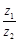 为纯虚数,则实数
为纯虚数,则实数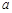 的值等于 .
的值等于 .
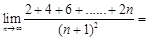 .
.
函数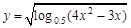 的定义域为 .
的定义域为 .
在等比数列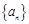 中,
中,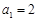 ,前
,前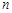 项和为
项和为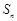 ,若数列
,若数列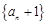 也是等比数列,则
也是等比数列,则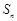 等于 .
等于 .
设直线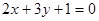 和圆
和圆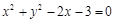 相交于点
相交于点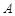 、
、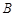 ,则弦
,则弦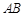 的垂直平分线方程是 .
的垂直平分线方程是 .
在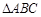 中,已知
中,已知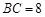 ,
,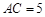 ,三角形面积为12,则
,三角形面积为12,则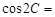 .
.
在极坐标系中,点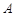 的极坐标为
的极坐标为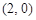 ,直线
,直线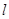 的极坐标方程为
的极坐标方程为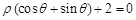 ,则点
,则点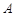 到直线
到直线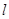 的距离等于 .
的距离等于 .
如果 的展开式中各项系数之和为128,则含
的展开式中各项系数之和为128,则含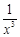 项的系数等于 .(用数字作答)
项的系数等于 .(用数字作答)
9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为0.5,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种。假定每个坑至多补种一次,每补种1个坑需10元,用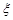 表示补种费用,则
表示补种费用,则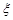 的数学期望值等于 .
的数学期望值等于 .
已知双曲线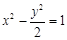 的焦点为
的焦点为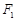 、
、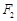 ,点
,点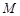 在双曲线上且
在双曲线上且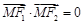 ,则点
,则点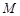 到
到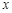 轴的距离等于 .
轴的距离等于 .
已知点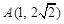 ,
,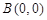 ,
,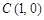 ,设
,设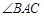 的平分线
的平分线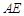 与
与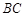 相交于
相交于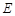 ,如果
,如果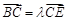 ,那么
,那么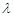 等于 .
等于 .
已知函数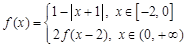 ,若方程
,若方程 在区间
在区间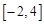 内有3个不等实根,则实数
内有3个不等实根,则实数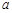 的取值范围是 .
的取值范围是 .
若数列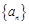 满足:存在正整数
满足:存在正整数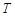 ,对于任意正整数
,对于任意正整数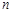 都有
都有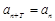 成立,则称数列
成立,则称数列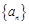 为周
为周
期数列,周期为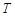 .已知数列
.已知数列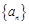 满足
满足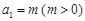 ,
,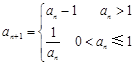 有以下结论:
有以下结论:
①若 ,则
,则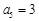 ;
;
②若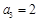 ,则
,则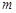 可以取3个不同的值;
可以取3个不同的值;
③若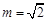 ,则
,则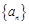 是周期为3的数列;
是周期为3的数列;
④存在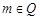 且
且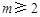 ,数列
,数列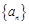 是周期数列.
是周期数列.
其中正确结论的序号是 (写出所有正确命题的序号).
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.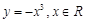 |
B.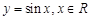 |
C.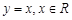 |
D.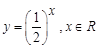 |
设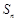 是等差数列
是等差数列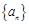 的前
的前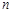 项和,若
项和,若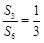 ,则
,则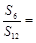 ( )
( )
A.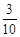 |
B.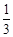 |
C.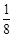 |
D.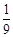 |
如图,已知圆锥的底面半径为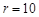 ,点
,点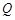 为半圆弧
为半圆弧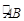 的中点,点
的中点,点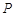 为母线
为母线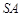 的中点.若
的中点.若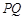 与
与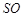 所成角为
所成角为 ,则此圆锥的全面积与体积分别为( )
,则此圆锥的全面积与体积分别为( )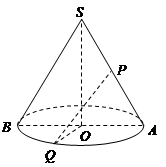
A.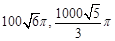 |
B.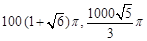 |
C.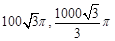 |
D.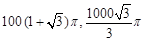 |
设函数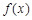 的图像关于点
的图像关于点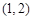 对称,且存在反函数
对称,且存在反函数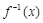 ,若
,若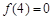 ,则
,则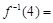 ( )
( )
| A.0 | B.4 | C.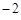 |
D.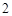 |
本题共有2小题,第(1)小题满分6分,第(2)小题满分6分.
已知函数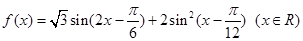 .
.
(1)化简并求函数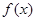 的最小正周期;
的最小正周期;
(2)求使函数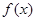 取得最大值的
取得最大值的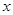 集合.
集合.
本题共有2小题,第(1)小题满分6分,第(2)小题满分8分.
如图,在长方体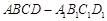 中,
中,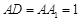 ,
,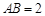 ,点
,点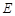 在棱
在棱 上移动.
上移动.
(1)证明: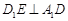 ;
;
(2)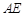 等于何值时,二面角
等于何值时,二面角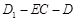 的大小为
的大小为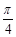 .
.
本题共有2小题,第(1)小题满分6分,第(2)小题满分8分.
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用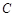 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度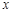 (单位:cm)满足关系:
(单位:cm)满足关系: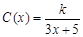
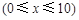 ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求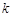 的值及
的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.
本题共有3小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分6分.
已知椭圆的中心在坐标原点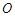 ,焦点在
,焦点在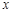 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点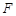 与
与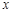 轴不垂直的直线交椭圆于
轴不垂直的直线交椭圆于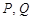 两点.
两点.
(1)求椭圆的方程;
(2)当直线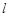 的斜率为1时,求
的斜率为1时,求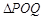 的面积;
的面积;
(3)在线段 上是否存在点
上是否存在点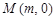 ,使得以
,使得以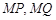 为邻边的平行四边形是菱形?若存在,求出
为邻边的平行四边形是菱形?若存在,求出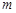 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
本题共有3小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
已知无穷等比数列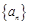 公比为
公比为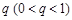 ,各项的和等于9,数列
,各项的和等于9,数列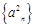 各项的和为
各项的和为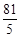 .对给定的
.对给定的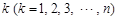 ,设
,设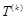 是首项为
是首项为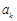 ,公差为
,公差为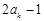 的等差数列.
的等差数列.
(1)求数列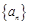 的通项
的通项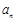 ;
;
(2)求数列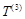 的前10项之和;
的前10项之和;
(3)设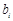 为数列
为数列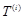 的第
的第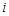 项,
项,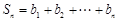 ,求正整数
,求正整数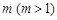 ,使得
,使得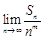 存在且不等于零.
存在且不等于零.