已知集合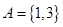 ,
,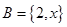 ,若
,若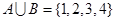 ,则
,则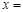 .
.
设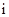 为虚数单位,则复数
为虚数单位,则复数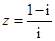 的虚部是 .
的虚部是 .
某课题组进行城市空气质量监测,按地域将30个城市分成甲、乙、丙三组,对应地域城市数分别为5、15、10.若用分层抽样抽取6个城市,则丙组中应该抽取的城市数为 .
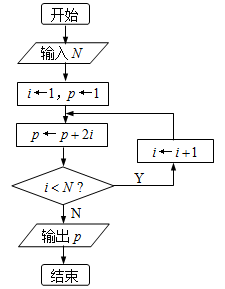
执行下边的程序框图,若输入的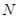 是
是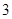 ,则输出
,则输出 的值是 .
的值是 .
从1、2、3、4这4个数中一次性随机地取两个数,则所取两个数的和为4或5的概率为 .
若等差数列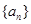 的前5项和
的前5项和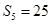 ,且
,且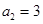 ,则
,则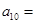 .
.
已知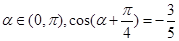 ,则
,则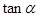 = .
= .
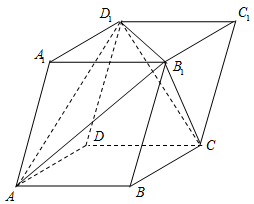
如图,已知四棱柱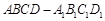 的体积为1,则截去三棱锥
的体积为1,则截去三棱锥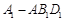 和三棱锥
和三棱锥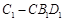 所得的多面体
所得的多面体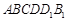 的体积为 .
的体积为 .
双曲线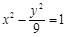 的渐近线与抛物线
的渐近线与抛物线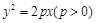 的准线相交于
的准线相交于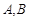 两点,若
两点,若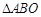 的面积为6(
的面积为6(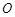 为坐标原点),则
为坐标原点),则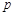 的值是 .
的值是 .
在边长为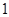 的等边
的等边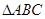 中,
中,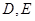 分别在边
分别在边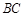 与
与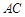 上,且
上,且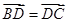 ,
,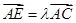
 ,若
,若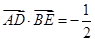 ,则
,则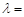 .
.
曲线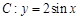 在
在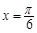 和
和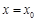 处的切线互相垂直,将曲线
处的切线互相垂直,将曲线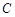 的图象向左平移
的图象向左平移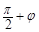 个单位后所得的图象关于直线
个单位后所得的图象关于直线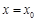 对称,则
对称,则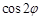 的值为 .
的值为 .
已知函数 的图象关于点
的图象关于点 中心对称,设关于
中心对称,设关于 的不等式
的不等式 的解集为
的解集为 ,若
,若 ,则正数
,则正数 的值是 .
的值是 .
已知函数 ,若方程
,若方程 有四个不同的实数解,则实数
有四个不同的实数解,则实数 的取值范围是 .
的取值范围是 .
已知集合 ,集合
,集合 ,
, ,若
,若 中存在元素
中存在元素 ,
, 中存在元素
中存在元素 ,使得
,使得 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
(本小题满分14分)在△ABC中,内角A,B,C的对边分别为a,b,c,若 .
.
(1)求 的值;
的值;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(本小题满分14分)如图,已知斜三棱柱 中,
中, ,
, 为
为 的中点.
的中点.
(1)若 ,求证:
,求证: ;
;
(2)求证: ∥平面
∥平面 .
.
(本小题满分14分)某市近郊有一块大约 的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别用 表示
表示 和S的函数关系式,并给出定义域;
和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值.
(本小题满分16分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且 APB面积的最大值为2
APB面积的最大值为2 .
.
(1)求椭圆C的方程及离心率;
(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.
(本小题满分16分)对于给定数列 ,如果存在实常数
,如果存在实常数 使得
使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “线性数列”.
是 “线性数列”.
(1)若 ,
, ,
, ,数列
,数列 、
、 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列 是“线性数列”,则数列
是“线性数列”,则数列 也是“线性数列”;
也是“线性数列”;
(3)若数列 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列 前
前 项的和.
项的和.
(本小题满分16分)已知函数 在
在 处的切线
处的切线 与直线
与直线 平行.
平行.
(1)求实数 的值;
的值;
(2)若关于 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)记函数 ,设
,设 是函数
是函数 的两个极值点,若
的两个极值点,若 ,且
,且 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
(本小题满分10分)如图所示,已知 为圆
为圆 的直径,
的直径, ,
, 是圆
是圆 上的两个点,
上的两个点, 于
于 ,
, 交
交 于
于 ,交
,交 于
于 ,
, .
.
(1)求证: 是劣弧
是劣弧 的中点;
的中点;
(2)求证: .
.
(本小题满分10分)已知矩阵 ,矩阵
,矩阵 ,直线
,直线 经矩阵
经矩阵 所对应的变换得到直线
所对应的变换得到直线 ,直线
,直线 又经矩阵
又经矩阵 所对应的变换得到直线
所对应的变换得到直线 .
.
(1)求 的值;
的值;
(2)求直线 的方程.
的方程.
(本小题满分10分)在极坐标中,已知点 为方程
为方程 所表示的曲线上一动点,点
所表示的曲线上一动点,点 的坐标为
的坐标为 ,求
,求 的最小值.
的最小值.
(本小题满分10分)已知 ,
, ,求证:
,求证: .
.
(本小题满分10分)如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面 ,
, ,
, 是
是 的中点,作
的中点,作 交
交 于点
于点 .
.
(1)求异面直线 与
与 所成角的大小;
所成角的大小;
(2)求二面角 的正弦值.
的正弦值.
(本小题满分10分)设 是给定的正整数,有序数组(
是给定的正整数,有序数组( )中
)中 或
或
 .
.
(1)求满足“对任意的 ,
, ,都有
,都有 ”的有序数组(
”的有序数组( )的个数
)的个数 ;
;
(2)若对任意的 ,
, ,
, ,都有
,都有 成立,求满足“存在
成立,求满足“存在 ,使得
,使得 ”的有序数组(
”的有序数组( )的个数
)的个数 .
.