已知集合
，则
．
3张卡片上分别写有数字0，1，2，从这3张卡片中一次随机抽取不同的2张，则取出的两张卡片上的数字之差的绝对值等于1的概率为 ．
已知幂函数
的在
上单调递增，则实数m的值为： ．
已知角
的终边经过点
，则角的正弦值 ．
函数
的图象关于直线
对称，则
= ．
下图为求
的程序框图，其中①应填 ．
若不等式组
表示的平面区域是一个四边形，则实数
的取值范围是 ．
若曲线
在点
处的切线与两条坐标轴围成的三角形的面积为
，则
．
已知奇函数
满足
，且当
时， 
，则
的值为 ．
函数
由下表定义：
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
若
，
，
，则
．
已知抛物线型拱桥的顶点距水面
米时，量得水面宽为
米．则水面升高
米后，水面宽是 米（精确到
米）．
已知平面向量
，
，
，
，
；则与的夹角是 ．
设向量
，记
，函数
的最大值是 ．
双曲线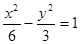
的渐近线与圆
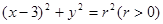相切，则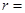
．
在锐角
中，已知内角
，
，
所对的边分别为
，
，
，向量
，
，且向量
共线．
（1）求角的大小；
（2）如果
，求的周长的最大值．
如下图所示，在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AB＝5，AA1＝4，点D是AB的中点．
（1）求证：AC⊥BC1；
（2）求证：AC1∥平面CDB1；
（3）求三棱锥
的体积．
2010年上海世博会某国要建一座八边形（不一定为正八边形）的展馆区（如图），它的主体造型的平面图是由二个相同的矩形
和
构成的面积为
m2的十字型地域，计划在正方形
上建一座“观景花坛”，造价为
元／m2，在四个矩形上（图中阴影部分）铺花岗岩地坪，造价为
元/m2,再在四个空角（如
等）上铺草坪，造价为
元/m2．设总造价为
元，
长为
m．
（1）试建立与的函数关系
（2）当为何值时，最小？并求这个最小值
已知直线
，一个圆的圆心
在
轴正半轴上，且该圆与直线
和
轴均相切．
（1）求该圆的方程；
（2）直线
与圆交于
两点，且
是等边三角形，求
的值．
已知数列
满足
，
．
（1）求证：数列
是等差数列；
（2）设
，数列
的前
项之和为
，求的最小值．
已知函数
，
，直线
与曲线
切于点
且与曲线
切于点
．
（1）求a，b的值和直线的方程；
（2）证明：
．
如图，
内接于圆
，
平分
交圆于点
，过点
作圆的切线交直线于点
．求证：
．
二阶矩阵M对应的变换将点（1，－1）与（－2，1）分别变换成点（－1，－1）与（0，－2）．
（Ⅰ）求矩阵M；
（Ⅱ）设直线
在变换M作用下得到了直线m：2x－y=4，求的方程
在极坐标系中，已知直线l的极坐标方程为
，圆C的圆心是
，半径为
。
（Ⅰ）求圆C的极坐标方程；
（Ⅱ）求直线l被圆C所截得的弦长
，证明：
．
已知函数
，
，直线
与曲线
切于点
且与曲线
切于点
．
（1）求a，b的值和直线的方程；
（2）证明：
．
已知在四棱锥
中，底面
是矩形，且
，
，
平面，
、
分别是线段
、
的中点．
（1）证明：
（2）若
与平面所成的角为
，求二面角
的余弦值
抛物线M：
的准线过椭圆N：
的左焦点，以坐标原点为圆心，以t（t>0）为半径的圆分别与抛物线M在第一象限的部分以及y轴的正半轴相交于点A与点B，直线AB与x轴相交于点C．
（1）求抛物线M的方程．
（2）设点A的横坐标为x1，点C的横坐标为x2，曲线M上点D的横坐标为x1+2，求直线CD的斜率．