设复数 ,
, 在复平面内的对应点关于虚轴对称,
在复平面内的对应点关于虚轴对称, ,则
,则 ( )
( )
| A.-5 | B.5 | C.-4+i | D.-4-i |
已知全集 ,
, ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
已知 分别是定义在
分别是定义在 上的偶函数和奇函数,且
上的偶函数和奇函数,且 ,则
,则 ( )
( )
A. |
B. |
C.1 | D.3 |
命题“ ”的否定是( )
”的否定是( )
A. |
B. |
C. |
D. |
已知 ,
, ,则( )
,则( )
A. |
B. |
C. |
D. |
已知向量 满足
满足 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
在同一直角坐标系中,函数 的图像可能是( )
的图像可能是( )

参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,可见部分信息如下,据此计算得到:参加数学抽测的人数 、分数在
、分数在 内的人数分别为( )
内的人数分别为( )

A. |
B. |
C. |
D. |
已知 满足
满足 ,且目标函数
,且目标函数 的最小值为
的最小值为 ,则实数
,则实数 的值是( )
的值是( )
A. |
B. |
C. |
D. |
已知双曲线 (
( )的渐近线与圆
)的渐近线与圆 相切,则双曲线的离心率为( )
相切,则双曲线的离心率为( )
A. |
B. |
C. |
D. |
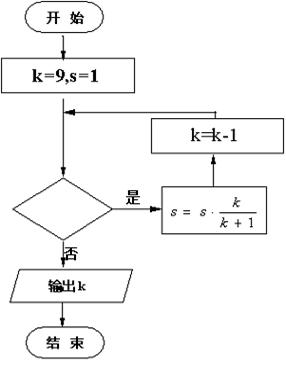
执行如图所示的程序框图,若输出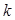 的值为6,则判断框内可填入的条件是 .
的值为6,则判断框内可填入的条件是 .
函数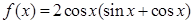 的最小值为 .
的最小值为 .
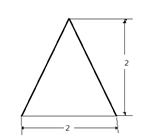
一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示该四棱锥体积是 .
已知圆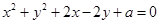 截直线
截直线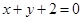 所得弦的长度为
所得弦的长度为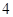 ,则实数
,则实数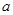 的值为 .
的值为 .
下列命题中,正确的是 .
(1)曲线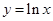 在点
在点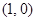 处的切线方程是
处的切线方程是 ;
;
(2)函数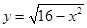 的值域是
的值域是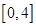 ;
;
(3)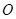 是
是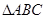 所在平面上一定点,动点P满足:
所在平面上一定点,动点P满足: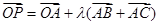 ,
,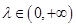 ,则
,则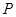 点的轨迹一定通过
点的轨迹一定通过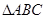 的重心;
的重心;
(本小题满分12分)设为 的内角
的内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 的最值.
的最值.
(本小题满分12分)如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, ,
, 为
为 与
与 的交点,
的交点, 为棱
为棱 上一点.
上一点.
(Ⅰ)证明:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)若 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分)为了了解山东省各旅游景点在大众中的熟知度,随机对15~65岁的人群抽样调查了 人,回答问题“山东省有哪几个著名的旅游景点?”统计结果如下图表.
人,回答问题“山东省有哪几个著名的旅游景点?”统计结果如下图表.
| 组号 |
分组 |
回答正确的人数 |
回答正确的人数 占本组的频率 |
| 第1组 |
[15,25) |
a |
0.5 |
| 第2组 |
[25,35) |
18 |
x |
| 第3组 |
[35,45) |
b |
0.9 |
| 第4组 |
[45,55) |
9 |
0.36 |
| 第5组 |
[55,65] |
3 |
y |

(1)分别求出 的值;
的值;
(2)从第 组回答正确的人中用分层抽样的方法抽取6人,求第
组回答正确的人中用分层抽样的方法抽取6人,求第 组每组各抽取多少人?
组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
(本小题满分12分)已知各项均为正数的数列 的前
的前 项和为
项和为 ,且
,且 .在数列
.在数列 中,
中, ,
, .
.
(Ⅰ)求 ,
, ;
;
(Ⅱ)设 求数列
求数列 的前项和
的前项和 .
.
(本小题满分13分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且 APB面积的最大值为2
APB面积的最大值为2 .
.
(1)求椭圆C的方程及离心率;
(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.

(本小题满分14分)
(1)当 时,求
时,求 的极值点.
的极值点.
(2)若 ,
, 的图象与
的图象与 的图象有
的图象有 个不同的交点,求实数
个不同的交点,求实数 的范围.
的范围.