复平面内表示复数 的点位于( )
的点位于( )
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
设集合 ,
,
 ,则
,则 =( )
=( )
A. |
B. |
C. |
D. |
已知定义在 上的奇函数
上的奇函数 满足
满足 ,若
,若 ,
, ,则实数
,则实数 的取值范围为( )
的取值范围为( )
A. |
B. |
C. |
D. |
已知命题 对任意
对任意 ,总有
,总有 ;
; 是
是 的充分不必要条件则下列命题为真命题的是( )
的充分不必要条件则下列命题为真命题的是( )
A. |
B. |
C. |
D. |
某几何体三视图如图所示,则该几何体的体积为( )

A. |
B. |
C. |
D. |
设常数 .则
.则  的二项展开式中
的二项展开式中 项的系数( ).
项的系数( ).
A. |
B. |
C. |
D. |
 满足约束条件
满足约束条件 ,若
,若 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数 的值为( )
的值为( )
A. |
B. |
C.2或1 | D. |
现有某病毒记作 其中正整数
其中正整数 、
、 (
( )可以任意选取,则
)可以任意选取,则 、
、 都取到奇数的概率为( )
都取到奇数的概率为( )
A. |
B. |
C. |
D. |
同时具有性质“⑴ 最小正周期是 ;⑵ 图象关于直线
;⑵ 图象关于直线 对称;⑶ 在
对称;⑶ 在 上是减函数”的一个函数可以是( )
上是减函数”的一个函数可以是( )
A. |
B. |
C. |
D. |
设直线 与双曲线
与双曲线 (
( )两条渐近线分别交于点
)两条渐近线分别交于点 ,若点
,若点 满足
满足 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. |
B. |
C. |
D. |
设 是一个各位数字都不是0且没有重复数字的三位数.将组成
是一个各位数字都不是0且没有重复数字的三位数.将组成 的3个数字按从小到大排成的三位数记为
的3个数字按从小到大排成的三位数记为 ,按从大到小排成的三位数记为
,按从大到小排成的三位数记为 (例如
(例如 ,则
,则 ,
, ).阅读如图所示的程序框图,运行相应的程序,任意输入一个
).阅读如图所示的程序框图,运行相应的程序,任意输入一个 ,输出的结果
,输出的结果 .
.

已知菱形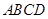 的边长为2,
的边长为2,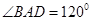 ,点
,点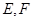 分别在边
分别在边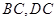 上,
上,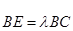 ,
,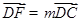 .若
.若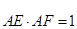 ,
,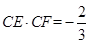 ,则
,则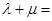 .
.
过抛物线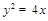 的焦点
的焦点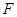 的直线
的直线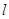 ,与圆
,与圆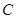 :
: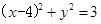 相交于A,B两点,且
相交于A,B两点,且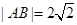 ,则
,则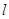 的方程是 .
的方程是 .
定义:分子为1且分母为正整数的分数叫做单位分数.我们可以把1拆分为无穷多个不同的单位分数之和.例如: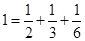 ,
,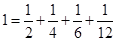 ,
,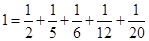 ,依此方法可得:
,依此方法可得: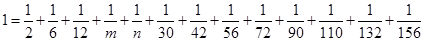 ,其中
,其中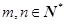 ,则
,则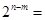 .
.
对定义在区间D上的函数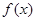 和
和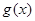 ,如果对任意
,如果对任意 ,都有
,都有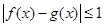 成立,那么称函数
成立,那么称函数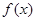 在区间D上可被
在区间D上可被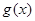 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
①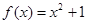 在区间
在区间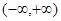 上可被
上可被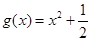 替代;
替代;
②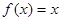 可被
可被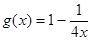 替代的一个“替代区间”为
替代的一个“替代区间”为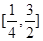 ;
;
③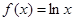 在区间
在区间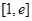 可被
可被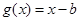 替代,则
替代,则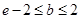 ;
;
④ ,则存在实数
,则存在实数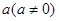 ,使得
,使得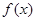 在区间
在区间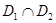 上被
上被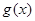 替代;其中真命题的有 .
替代;其中真命题的有 .
(本小题满分12分)已知 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量 ,
, ,且
,且 .
.
(1)求角A的大小;
(2)若 ,求
,求
(本小题满分12分)如图,在多面体 中,底面
中,底面 是边长为
是边长为 的的菱形,
的的菱形, ,四边形
,四边形 是矩形,平面
是矩形,平面 平面
平面 ,
, ,
, 和
和 分别是
分别是 和
和 的中点.
的中点.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求二面角 的大小.
的大小.
(本小题满分12分)某市公租房的房源位于 三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任意4位申请人中:
三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任意4位申请人中:
(1)恰有2人申请 片区房源的概率;
片区房源的概率;
(2)申请的房源所在片区的个数 的分布列和期望.
的分布列和期望.
(本小题满分12分)已知数列 是等比数列,首项
是等比数列,首项 ,公比
,公比 ,其前
,其前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
, 为数列
为数列 的前
的前 项和,若
项和,若 恒成立,求
恒成立,求 的最大值.
的最大值.
(本小题满分13分)已知实数 ,函数
,函数 .
.
(1)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若当 时,函数
时,函数 图象上的点均在不等式
图象上的点均在不等式 ,所表示的平面区域内,求实数
,所表示的平面区域内,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆
 的右焦点为
的右焦点为 ,且点
,且点 在椭圆
在椭圆 上,
上, 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设过定点 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 、
、 ,且
,且 为锐角,求直线
为锐角,求直线 的斜率
的斜率 的取值范围;
的取值范围;
(Ⅲ)过椭圆
 上异于其顶点的任一点
上异于其顶点的任一点 ,作圆
,作圆
 的两条切线,切点分别为
的两条切线,切点分别为 (
( 不在坐标轴上),若直线
不在坐标轴上),若直线 在
在 轴、
轴、 轴上的截距分别为
轴上的截距分别为 、
、 ,证明:
,证明: 为定值.
为定值.