若复数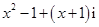
是纯虚数（i是虚数单位，
），则
（ ）
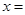| A．1 | B．-1 | C． |
D．0 |
已知集合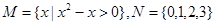
，则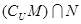
=（ ）
A． |
B． |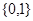
C． |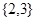
D． |
下列函数中，在区间
上为增函数的是（ ）
A． |
B． |
C． |
D． |
阅读如图所示的程序框图，运行相应的程序．若输出的S 为
，则判断框中填写的内容可以是 （ ）
A． |
B． |
C． |
D． |
如图，网格纸上小正方形的边长为
，粗线画出的是某多面体的三视图，则该多面体的表面积为（ ）
A．48 |
B． |
C．48 | D． |
已知
=
，且
，则则向量与向量
的夹角为（ ）
A． |
B． |
C． |
D． |
已知△
中，内角A，B，C的对边分别为
,
，
，则△的面积为（ ）
A． |
B．1 | C． |
D．2 |
已知函数
，则函数
的部分图象可以为 （ ）
已知双曲线
与函数的图象交于
点
．若函数
在点处的切线过双曲线左焦点
，则双曲线的离心率是（ ）
A． |
B． |
C． |
D． |
若对
，不等式
恒成立，则实数
的最大值是（ ）
A． |
B．1 | C．2 | D． |
函数
（
）的单调递增区间是__________．
在平面直角坐标系xOy中，已知A、B分别是双曲线
的左、右焦点，△ABC 的顶点C在双曲线的右支上，则
的值是
已知等比数列
的前
项和
，则的通项公式是 ．
设
,
，则
的最小值是 ．
同底的两个正三棱锥内接于同一个球．已知两个正三棱锥的底面边长为a，球的半径为R．设两个正三棱锥的侧面与底面所成的角分别为
、
，则
的值是 ．
（本小题满分12分）已知函数
,其中
．
（Ⅰ）求
最小正周期及对称轴方程；
（Ⅱ）在锐角
中,内角
的对边分别为
，已知
,
，求
边上的高
的最大值．
（本小题满分12分）已知
的三个角
的对边分别为
，且成等差数列，且
。数列
是等比数列，且首项
，公比为
。
（1）求数列的通项公式；
（2）若
，求数列
的前
项和
．
（本小题满分12分）若定义在
上的函数
满足
，
，
R．
（Ⅰ）求函数解析式；
（Ⅱ）求函数
单调区间．
（本小题满分12分）如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠DAB＝
，PD⊥平面ABCD，PD=AD=1，点
分别为AB和PD中点．
（Ⅰ）求证：直线AF
平面PEC ；
（Ⅱ）求PC与平面PAB所成角的正弦值．
（本小题满分13分）某校A,B两个班级各有5名编号为1，2，3，4，5的学生进行射击训练，每人射击10次，击中的次数统计如下表：
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| A班 |
9 |
7 |
8 |
6 |
5 |
| B班 |
7 |
8 |
9 |
7 |
4 |
（Ⅰ）从统计数据看，A,B两个班哪个班成绩更稳定（用数据说明）？
（Ⅱ）在本次训练中，从两班中分别任选一个同学，比较两人的击中次数，求A班同学击中次数低于B班同学击中次数的概率．
（本小题满分14分）已知椭圆
:
的上顶点为
，且离心率为
．
（Ⅰ）求椭圆的方程；
（Ⅱ）证明：过椭圆
:
上一点
的切线方程为
；
（Ⅲ）从圆
上一点
向椭圆引两条切线，切点分别为
,当直线
分别与
轴、
轴交于
、
两点时，求
的最小值．