若集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
函数 (
( R,
R, )的最小正周期为
)的最小正周期为 ,为了得到
,为了得到 的图象,只需将函数
的图象,只需将函数 的图象( ).
的图象( ).
A.向左平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向右平移 个单位长度 个单位长度 |
同时掷 个骰子,其中最大点数为
个骰子,其中最大点数为 ,则
,则 ( )(
( )( 1,2,3,4,5,6)
1,2,3,4,5,6)
A. |
B. |
C. |
D. |
从椭圆 上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
A. |
B. |
C. |
D. |
对任意非零实数 ,定义
,定义 的算法原理如右侧程序框图所示.设
的算法原理如右侧程序框图所示.设 ,
, ,则计算机执行该运算后输出的结果是( )
,则计算机执行该运算后输出的结果是( )
A. |
B. |
C. |
D. |
若实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( )
A. |
B.2 | C. |
D. |
“直线l1: ax+2y-8=0与直线l2: x+(a+1)y+4=0平行”是 “ ”的 ( )
”的 ( )
| A.充分而不必要 |
| B.必要而不充分 |
| C.充要条件 |
| D.既不充分也不必要条件 |
下列命题中的假命题是( )
| A.x∈R,lgx=0 |
| B.x∈R,tanx=2 |
| C.x∈R,2x>0 |
D.x∈R, >1 >1 |
若正项数列 满足
满足 ,且
,且 ,则
,则 的值为( )
的值为( )
| A.2015×1010 | B.2015×1011 |
| C.2016×1010 | D.2016×1011 |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A.( ) ) |
B.( ) ) |
C.( ) ) |
D.( ) ) |
在△ABC中,已知 ,
, ,则
,则 的值为 .
的值为 .
设i是虚数单位,z(1+i)=4+2i,则z的共轭复数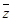 = .
= .
设函数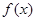 定义域为
定义域为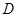 ,若存在非零实数
,若存在非零实数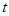 ,使得对任意
,使得对任意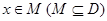 ,都有
,都有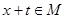 ,且
,且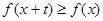 成立,则称
成立,则称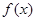 为
为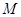 上的“
上的“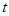 频函数”.若
频函数”.若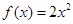 为区间
为区间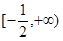 上的“
上的“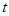 频函数”,则
频函数”,则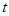 的取值范围是 .
的取值范围是 .
某几何体的三视图如图,则它的体积是________.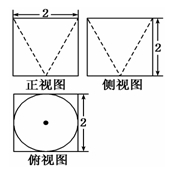
函数f(x)上任意一点A(x1,y1)处的切线l1.在其图像上总存在异与点A的点B(x2,y2),使得在点B处的切线l2满足l1// l2.则称函数具有“自平行性”.下列有关函数f(x)的命题:
①函数f(x)=sinx+1具有“自平行性” ②函数f(x)=x3(1≤x≤2)具有“自平行性”
③函数f(x)=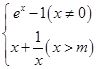 具有“自平行性”的充要条件为函数m=1;
具有“自平行性”的充要条件为函数m=1;
④ 奇函数y= f(x) (x≠0)不一定具有“自平行性” ⑤偶函数y= f(x)具有“自平行性”
其中所有叙述正确的命题的序号是 .
(本小题满分12分)在△ABC中,内角A,B,C的对边分别是 ,
, ,
, ,已知
,已知 ,sinA-sinC=sin(A-B).
,sinA-sinC=sin(A-B).
(Ⅰ)求B;
(Ⅱ)若b=2 ,求△ABC的面积。
,求△ABC的面积。
(本小题满分12分)已知各项都不相等的等差数列{an}的前六项和为60,且a6为a1和a21的等比中项.
(1)求数列{an}的通项公an及前n项和Sn;
(2)若数列{bn}满足bn+1-bn=an(n∈N*),且b1=3,求数列{}的前n项和Tn.
(本小题满分12分)如图,四棱锥 的底面是正方形,
的底面是正方形, ⊥底面
⊥底面 ,点
,点 在棱
在棱 上.
上.
(Ⅰ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)当 且
且 为
为 的中点时,求
的中点时,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门.该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同.
(1)求3个学生选择了3门不同的选修课的概率;
(2)求恰有2门选修课这3个学生都没有选择的概率;
(3)设随机变量X为甲、乙、丙这三个学生选修数学史这门课的人数,求X的分布列.
(本小题满分13分)已知函数 ,其中
,其中 为常数.
为常数.
(1)当 时,若
时,若 在区间
在区间 上的最大值为
上的最大值为 ,求
,求 的值;
的值;
(2)当 时,若函数
时,若函数 存在零点,求实数
存在零点,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知焦点在 轴,顶点在原点的抛物线
轴,顶点在原点的抛物线 经过点
经过点 ,以抛物线
,以抛物线 上一点
上一点 为圆心的圆过定点
为圆心的圆过定点 (0,1),记
(0,1),记 为圆
为圆 与
与 轴的两个交点.
轴的两个交点.
(1)求抛物线 的方程;
的方程;
(2)当圆心 在抛物线上运动时,试判断
在抛物线上运动时,试判断 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心 在抛物线上运动时,记
在抛物线上运动时,记 ,
, ,求
,求 的最大值.
的最大值.