若集合M={y|y=2x},N={y| },则M∪N=( )
},则M∪N=( )
| A.{x|x>1} | B.{y|y≥1} | C.{x|x>0} | D.{y|y≥0} |
复数 在复平面内对应的点在实轴上,则实数
在复平面内对应的点在实轴上,则实数 的值是( )
的值是( )
A. |
B. |
C. |
D. |
已知函数 ,则
,则 ( )
( )
| A.-5 | B.3 | C.-1 | D.4 |
如图所示,程序框图(算法流程图)的输出结果是( )

A  B
B  C
C  D
D 
某几何体的三视图如图所示,则这个几何体的表面积为( )

A. |
B. |
C. |
D. |
已知双曲线 (
( >0,
>0,  >0)的离心率为2,一个焦点与抛物线
>0)的离心率为2,一个焦点与抛物线 的焦点相同,则双曲线的渐近线方程为( )
的焦点相同,则双曲线的渐近线方程为( )
A. |
B. |
C. |
D. |
将函数 的图象向左平移
的图象向左平移 个单位后,所得到的图象对应的函数为奇函数,则
个单位后,所得到的图象对应的函数为奇函数,则 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
已知定义在 上的函数
上的函数 满足:
满足: ,且
,且 ,
, ,则方程
,则方程 在区间
在区间 上的所有实根之和为( )
上的所有实根之和为( )
| A.-7 | B.-8 | C.-6 | D.-5 |
已知正项数列 的前
的前 项和为
项和为 ,且
,且 ,则数列
,则数列 的通项公式为
的通项公式为 =( )
=( )
A. |
B. |
C. |
D. |
对于R上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有( ).
| A.f(0)+f(2)<2f(1) | B.f(0)+f(2)≤2f(1) |
| C.f(0)+f(2)≥2f(1) | D.f(0)+f(2)>2f(1) |
已知变量x,y满足约束条件 ,若
,若 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
| A.(0,1] | B.(0,1) | C. |
D.[0,1) |
已知 是
是 内一点且
内一点且 ,
, ,若
,若 的面积分别为
的面积分别为
 ,则
,则 的最小值是( )
的最小值是( )
A. |
B. |
C. |
D. |
如图,圆C内切于扇形AOB,∠AOB=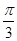 ,若在扇形AOB内任取一点,则该点在圆C内的概率为_________.
,若在扇形AOB内任取一点,则该点在圆C内的概率为_________.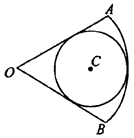
下列命题中正确的是( )
①若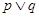 为真命题,则
为真命题,则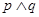 为真命题
为真命题
②“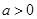 ,
,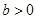 ”是“
”是“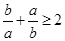 ”的充分必要条件
”的充分必要条件
③命题“若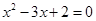 ,则
,则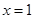 或
或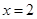 ”的逆否命题为“若
”的逆否命题为“若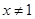 或
或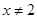 ,则
,则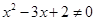 ”
”
④命题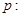
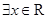 ,使得
,使得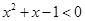 ,则
,则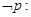
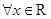 ,使得
,使得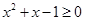
上述命题中不正确的是_______.
已知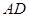 为△ABC内角
为△ABC内角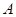 的角平分线,
的角平分线,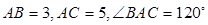 ,则
,则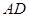 的长为_____.
的长为_____.
定义:如果函数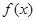 在
在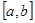 上存在
上存在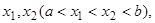 满足
满足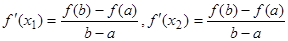 ,则称函数
,则称函数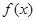 是
是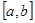 上的“DM函数”。已知函数
上的“DM函数”。已知函数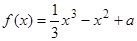 是
是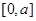 上“DM函数”,则实数
上“DM函数”,则实数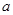 的取值范围是______.
的取值范围是______.
已知数列 的前n项和
的前n项和 (其中c,k为常数),且
(其中c,k为常数),且 2=4,
2=4, 6=8
6=8 3
3
(Ⅰ)求 ;
;
(Ⅱ)求数列 的前n项和Tn.
的前n项和Tn.
已知函数 的最大值为了3,函数
的最大值为了3,函数 的图象的相邻两对称轴间的距离为2,在
的图象的相邻两对称轴间的距离为2,在 轴上的截距为2。
轴上的截距为2。
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调递增区间。
的单调递增区间。
如图所示,在正方体 中,
中, 分别是棱
分别是棱 的中点.
的中点.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)证明: //平面
//平面 ;
;
(Ⅲ)若正方体棱长为1,求四面体 的体积.
的体积.
(本小题满分12分)已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:
若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示数学成绩与地理成绩,例如:表中数学成绩为B等级的共有20+18+4=42人,已知x与y均为B等级的概率是0.18.
(1)若在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩为C等级的学生中,已知a≥10,b≥8,求数学成绩为A等级的人数比C等级的人数少的概率.
已知椭圆 的离心率为
的离心率为 ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线 的焦点重合,过点
的焦点重合,过点 且不垂直于
且不垂直于 轴的直线
轴的直线 与椭圆
与椭圆 相交于
相交于 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)求 的取值范围.
的取值范围.
已知函数 的图像在点
的图像在点 (e为自然对数的底数)处切线斜率为3.
(e为自然对数的底数)处切线斜率为3.
求实数 的值;
的值;
若 且
且 对任意
对任意 恒成立,求k的最大值。
恒成立,求k的最大值。