若复数z满足(1+i)z=2-z,则|z+i|=( ).
A. |
B. |
C.2 | D. |
已知三棱锥的三视图,则该三棱锥的侧面积是 ( )

A. |
B. |
C. |
D. |
已知 中,
中, ,且
,且 的面积为
的面积为 ,则
,则 ( )
( )
A. |
B. |
C. 或 或 |
D. 或 或 |
已知定义在 上的函数
上的函数 满足:
满足: ,且
,且 ,
, ,则方程
,则方程 在区间
在区间 上的所有实根之和为( )
上的所有实根之和为( )
| A.-7 | B.-8 | C.-6 | D.-5 |
如图所示,程序框图(算法流程图)的输出结果是( )

A. |
B. |
C. |
D. |
已知正项数列 的前
的前 项和为
项和为 ,且
,且 ,则数列
,则数列 的通项公式为
的通项公式为 =( )
=( )
A. |
B. |
C. |
D. |
已知偶函数 满足当x>0时,
满足当x>0时, ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
椭圆 两个焦点分别是
两个焦点分别是 ,点
,点 是椭圆上任意一点,则
是椭圆上任意一点,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
在中,角所对的边分别是,若,则的最小角的余弦值等于( )
A. B. C. D.
已知函数f(x)的定义域为R,且满足f(x+2)=-f(x).若f(x)为奇函数,且当0≤x≤1时,f(x)= x,求使f(x)=-
x,求使f(x)=- 在[0,2010]上的所有x的个数( )
在[0,2010]上的所有x的个数( )
| A.252 | B.502 | C.251 | D.501 |
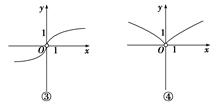
函数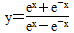 的图象大致为________.
的图象大致为________.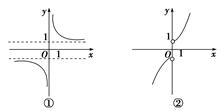
下列命题中正确的是
①若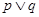 为真命题,则
为真命题,则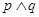 为真命题
为真命题
②“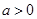 ,
,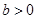 ”是“
”是“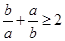 ”的充分必要条件
”的充分必要条件
③命题“若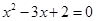 ,则
,则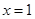 或
或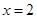 ”的逆否命题为“若
”的逆否命题为“若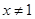 或
或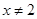 ,则
,则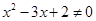 ”
”
④命题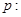
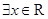 ,使得
,使得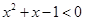 ,则
,则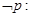
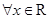 ,使得
,使得
上述命题中不正确的是_______
定义在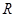 上的偶函数
上的偶函数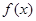 满足
满足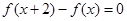 ,且在
,且在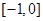 上单调递增,设
上单调递增,设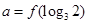 ,
,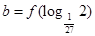 ,
,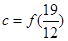 ,则
,则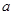 ,
,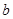 ,
,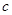 的大小关系是________
的大小关系是________
如图,矩形ABCD的四个顶点的坐标分别为A(0,—1),B(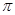 ,—1),C(
,—1),C(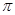 ,1),D(0,1),正弦曲线
,1),D(0,1),正弦曲线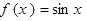 和余弦曲线
和余弦曲线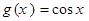 在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是__________
在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是__________
设函数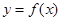 的定义域为
的定义域为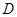 ,如果存在非零常数
,如果存在非零常数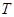 ,对于任意
,对于任意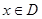 ,都有
,都有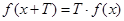 ,则称函数
,则称函数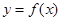 是类周期函数,非零常数
是类周期函数,非零常数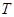 为函数
为函数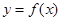 的类周期”.现有下面四个关于类周期函数的命题:
的类周期”.现有下面四个关于类周期函数的命题:
①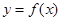 的类周期为-1,那么它是周期为2的周期函数;
的类周期为-1,那么它是周期为2的周期函数;
②若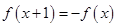 ,则
,则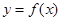 不是类周期函数;
不是类周期函数;
③函数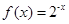 是类周期函数;
是类周期函数;
④如果函数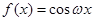 是类周期函数,那么
是类周期函数,那么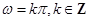 .
.
其中是真命题的有___________
已知锐角 的三个内角
的三个内角 所对的边分别为
所对的边分别为 .且
.且 。
。
(1)求角 的大小;
的大小;
(2)求 的取值范围.
的取值范围.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD
⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
(Ⅰ)求证:EF 平面PAD;
平面PAD;
(Ⅱ)求平面EFG与平面ABCD所成锐二面角的大小;
下图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
(Ⅰ)求该专业毕业总人数N和90~95分数段内的人数 ;
;
(Ⅱ)现欲将90~95分数段内的 名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为
名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为 ,求
,求 名毕业生中男女各几人(男女人数均至少两人)?
名毕业生中男女各几人(男女人数均至少两人)?
(Ⅲ)在(Ⅱ)的结论下,设随机变量 表示n名毕业生中分配往乙学校的三名学生中男生的人数,求
表示n名毕业生中分配往乙学校的三名学生中男生的人数,求 的分布列和数学期望.
的分布列和数学期望.
已知椭圆 的右焦点
的右焦点 ,离心率为
,离心率为 ,过
,过 作两条互相垂直的弦
作两条互相垂直的弦 ,设
,设 的中点分别为
的中点分别为 .
.
(1)求椭圆的方程;
(2)证明:直线 必过定点,并求出此定点坐标;
必过定点,并求出此定点坐标;
(3)若弦 的斜率均存在,求
的斜率均存在,求 面积的最大值.
面积的最大值.
已知函数 在
在 内有极值.
内有极值.
(Ⅰ)求实数的取值范围;
(Ⅱ)若 ,
, ,且
,且 时,求证:
时,求证:
(本小题满分7分)选修4—2:矩阵与变换
已知矩阵 ,试求曲线
,试求曲线 在矩阵
在矩阵 变换下的函数解析式.
变换下的函数解析式.
选修4—4:坐标系与参数方程
已知曲线 的参数方程:
的参数方程:  (
( 为参数), 曲线
为参数), 曲线 上的点
上的点 对应的参数
对应的参数 ,以坐标原点
,以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线 的极坐标方程;
的极坐标方程;
(Ⅱ)已知直线 过点P(1,0),且与曲线
过点P(1,0),且与曲线 于A,B两点,求
于A,B两点,求 的范围.
的范围.
(本小题满分7分)选修4—5:不等式选讲
已知a+b=1,对 ,b∈(0,+∞),
,b∈(0,+∞), +
+ ≥|2x-1|-|x+1|恒成立,
≥|2x-1|-|x+1|恒成立,
(Ⅰ)求 +
+ 的最小值;
的最小值;
(Ⅱ)求x的取值范围。