若集合A＝{x｜－3＜x＜1}，B＝{x｜0＜x＜2}，则集合A∩B＝（ ）．
| A．{x｜－1＜x＜1} | B．{x｜－3＜x＜1} |
| C．{x｜－3＜x＜2} | D．{x｜0＜x＜1} |
已知复数
，则
在复平面内对应的点位于（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
如图，一个几何体的三视图如图所示，则其体积为（ ）
A． |
B． |
C． |
D． |
在区间
上随机选取一个数M，不变执行如图所示的程序框图，且输入
的值为1，然后输出
的值为N，则
的概率为（ ）
A． |
B． |
C． |
D． |
若命题
：
；命题
：
，则下列结论正确的是（ ）
A． 为假命题 |
B． 为假命题 |
C． 为假命题 |
D． 为真命题 |
若
，则
的值使得过
可以做两条直线与圆
相切的概率等于（ ）
A． |
B． |
C． |
D．不确定 |
函数
是偶函数，则f（x）的最大值是（ ）
A． |
B． |
C． |
D． |
若函数
且
在
上既是奇函数又是增函数，则
的图象是
已知一个三棱柱，其底面是正三角形，且侧棱与底面垂直，一个体积为
的球与棱柱的所有面均相切，那么这个三棱柱的表面积是（ ）
A． |
B． |
C． |
D． |
已知平面向量
的夹角为
，且
，在
中，
，D为BC的中点，则
（ ）
| A．2 | B．4 | C．6 | D．8 |
已知点
在不等式组
表示的平面区域上运动，则
的取值范围是（ ）
A． |
B． |
C． |
D． |
对实数a与b，定义新运算“⊗”：a⊗b=
．设函数f（x）=（x2﹣2）⊗（x﹣1），x∈R．若函数y=f（x）﹣c的图象与x轴恰有两个公共点，则实数c的取值范围是（ ）
| A．（﹣1，1]∪（2，+∞） |
| B．（﹣2，﹣1]∪（1，2] |
| C．（﹣∞，﹣2）∪（1，2] |
| D．[﹣2，﹣1] |
如图，在半径为2的半圆内，放置一个边长为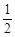
的正三角形ABC，向半圆内任投一点，该点落在正方形内的概率为_________．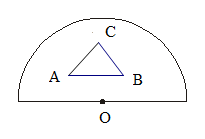
直线
与圆C：
没有公共点，则m的取值范围是_________．
已知
在
上单调递增，且
仅有一解，求实数p的取值范围_______
用
表示非空集合
中的元素个数，定义
，
若
，
，且
，则
（本小题满分12分）设数列
的前n项和为
,点
均在函数y=x-2的图像上．
（1）求数列的通项公式；
（2）求
；
（3）在（2）的条件下，求使得
对所有
都成立的最大整数m．
（本小题满分12分）已知函数
，且当
时，
的最小值为2，
（1）求
的值，并求的单调递增区间；
（2）先将函数
的图象上的点纵坐标不变，横坐标缩小到原来的
，再将所得的图象向右平移
个单位，得到函数
的图象，求方程
在区间
上所有根之和．
（本题12分）如图，在四棱锥E-ABCD中，AB⊥平面BCE,DC⊥平面BCE,AB=BC=CE=2CD=2，
；
（1）求证：平面ADE⊥平面ABE；
（2）求三棱锥A-BDE的体积．
（本小题满分12分）某学校有男老师45名，女老师15名，按照分层抽样的方法组建了一个4人的学科攻关小组。
（1）求某老师被抽到的概率及学科攻关小组中男、女老师的人数；
（2）经过一个月的学习、讨论，这个学科攻关小组决定选出2名老师做某项实验，方法是先从小组里选出1名老师做实验，该老师做完后，再从小组内剩下的老师中选1名做实验，求选出的2名老师中恰有1名女老师的概率．
（本小题满分12分）椭圆
过点
，离心率为
，左右焦点分别为
，过点
的直线交椭圆于
两点。
（1）求椭圆
的方程；
（2）当
的面积为
时，求
的方程．
（本小题满分14分）已知a>0,函数
．
（1）讨论函数f（x）的单调性；
（2）当函数f（x）存在极值时，设所有极值之和为g（a），求g（a）的取值范围．