设全集为 ,集合
,集合 ,
, ,则( )
,则( )
A. |
B. |
C. |
D. |
已知 是虚数单位,若
是虚数单位,若 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
“ ”是“函数
”是“函数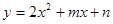 在
在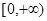 上单调”的( )
上单调”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列不等式中成立的是( )
A.若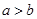 ,则 ,则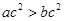 |
B.若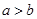 ,则 ,则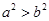 |
C.若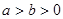 ,则 ,则 |
D.若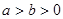 ,则 ,则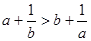 |
设 ,
, ,
, 为平面,
为平面, ,
, 为直线,则
为直线,则 的一个充分条件是( )
的一个充分条件是( )
A. , , , , |
B. , , , , |
C. , , , , |
D. , , , , |
某程序框图如图所示,若该程序运行后输出的值是 ,则( )
,则( )

A. |
B. |
C. |
D. |
已知圆 和两点
和两点 ,
, ,若圆
,若圆 上存在点
上存在点 ,使得
,使得 ,则
,则 的最大值为
的最大值为
A. |
B. |
C. |
D. |
已知x,y满足 且
且 的最大值与最小值分别为
的最大值与最小值分别为 和
和 ,则
,则 的值是( )
的值是( )
A. |
B. |
C.2 | D.4 |
已知 、
、 是双曲线
是双曲线 (
( )的左、右焦点,点
)的左、右焦点,点 关于渐近线的对称点恰好落在以
关于渐近线的对称点恰好落在以 为圆心,
为圆心, 为半径的圆上,则该双曲线的离心率为
为半径的圆上,则该双曲线的离心率为
A. |
B. |
C. |
D. |
若函数 满足对任意的
满足对任意的 ,都有
,都有 成立,则称函数
成立,则称函数 在区间
在区间 上是“被
上是“被 约束的”。若函数
约束的”。若函数 在区间
在区间 上是“被
上是“被 约束的”,则实数
约束的”,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知 ,且
,且 ,则
,则 的值为 .
的值为 .
某中学有男教职工200人,女教职工180人,现用分层抽样法从全体教职工中抽取19人参加座谈会,则男教职工应抽取的人数为___________.
【命题意图】本题主要考查简单随机抽样、分层抽样等基础知识,意在考查学生运算求解能力.
某几何体的三视图如图所示,其中俯视图是半圆,则该几何体的侧面积为 .

已知 ,则
,则 的最小值为
的最小值为
对于函数 ,有下列4个结论:
,有下列4个结论:
①任取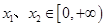 ,都有
,都有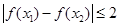 恒成立;
恒成立;
②
 ,对于一切
,对于一切 恒成立;
恒成立;
③函数 有3个零点;
有3个零点;
④对任意 ,不等式
,不等式 恒成立.
恒成立.
则其中所有正确结论的序号是 .
(本小题满分12分)已知函数
(Ⅰ)求函数 的对称中心;
的对称中心;
(Ⅱ)已知△ABC内角 的对边分别为
的对边分别为 ,且
,且 ,
, ,
, ,求
,求
(本小题满分12分)某市统计局就某地居民的月收入调查了 10 000 人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1500)).
(Ⅰ)求居民收入在[3 000,3 500)的频率;
(Ⅱ)根据频率分布直方图算出样本数据的中位数;
(Ⅲ)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这 10 000 人中按分层抽样方法抽出 100 人作进一步分析,则月收入在[2 500,3 000)的这段应抽取多少人?
如图,在三棱锥 中,平面
中,平面 平面
平面 ,
, 于点
于点 ,且
,且 ,
, ,
,

(1)求证:
(2)
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分) 已知单调递增的等比数列 满足:
满足: ,且
,且 是
是 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,求
,求 成立的正整数
成立的正整数 的最小值.
的最小值.
(本小题满分13分)已知椭圆 (
( )的左、右顶点分别为
)的左、右顶点分别为 ,
, ,且
,且 ,
, 为椭圆上异于
为椭圆上异于 ,
, 的点,
的点, 和
和 的斜率之积为
的斜率之积为 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设 为椭圆中心,
为椭圆中心, ,
, 是椭圆上异于顶点的两个动点,求
是椭圆上异于顶点的两个动点,求 面积的最大值.
面积的最大值.
(本小题满分14分)设函数 .
.
(1)若函数 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值;
(2)若存在 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.