设集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
当 时,复数
时,复数 在复平面内对应的点位于( )
在复平面内对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知等边三角形 的边长为
的边长为 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
下列函数中在其定义域内既是奇函数又是增函数的是( )
A. |
B. |
C. |
D. |
某几何体的三视图如图所示,若这个几何体的体积为 ,则
,则 ( )
( )

A. |
B. |
C. |
D. |
某一考场有64个试室,试室编号为001-064,现根据试室号,采用系统抽样法,抽取8个试室进行监控抽查,已抽看了005,021试室号,则下列可能被抽到的试室号是( )
| A.029,051 | B.036,052 | C.037,053 | D.045,054 |
执行如图所示程序框图,则其结果输出 为( )
为( )

A. |
B. |
C. |
D. |
对于实数 和
和 ,定义运算“
,定义运算“ ”:
”: ,设
,设 ,且关于
,且关于 的方程
的方程 恰有三个互不相等的实数根
恰有三个互不相等的实数根 ,
, ,
, ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
不等式 的解集为_________.
的解集为_________.
已知变量 、
、 满足约束条件
满足约束条件 ,且
,且 的最小值为_______.
的最小值为_______.
已知曲线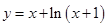 在点
在点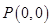 处切线与直线
处切线与直线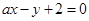 平行,则实数
平行,则实数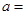 _______.
_______.
若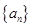 是等差数列,且
是等差数列,且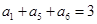 ,则数列
,则数列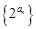 的前7项积
的前7项积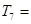 ________.
________.
二项展开式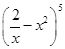 中,含
中,含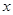 项的系数为 .(用数字作答)
项的系数为 .(用数字作答)
(坐标系与参数方程选做题)曲线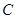 :
: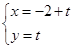 (
(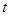 为参数),若以点
为参数),若以点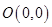 为极点,
为极点,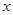 轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
(几何证明选讲选做题)如图,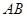 是圆
是圆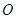 的直径,
的直径,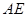 是圆内接
是圆内接 的高,若
的高,若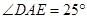 ,则
,则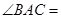 .
.

(本小题满分12分)已知函数 .
.
(1)求 的值;
的值;
(2)若 中,
中, ,
, ,求
,求 .
.
(本小题满分12分)甲、乙两人进行五局三胜制羽毛球决赛,除第五局两人获胜的机会相等外,其余各局甲获胜的概率都是 ,记
,记 为比赛的局数,每局比赛结果相互独立.
为比赛的局数,每局比赛结果相互独立.
(1)试求甲 获胜的概率,乙
获胜的概率,乙 获胜的概率;
获胜的概率;
(2)求 的分布列及数学期望值
的分布列及数学期望值 .
.
(本小题满分14分)如图,平面 平面
平面 ,其中
,其中 为正方形,
为正方形, 为直角梯形,
为直角梯形, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值大小.
的余弦值大小.
(本小题满分14分)已知数列 对任意的
对任意的 ,都有
,都有 且
且 .
.
(1)求 ,
, 的值;
的值;
(2)求数列 的通项公式
的通项公式 ;
;
(3)若 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
(本小题满分14分)已知直线 经过椭圆
经过椭圆 :
: 的右焦点和上顶点.
的右焦点和上顶点.
(1)求椭圆 的标准方程;
的标准方程;
(2)过点 的直线
的直线 与椭圆
与椭圆 交于不同的
交于不同的 、
、 两点,若
两点,若 为钝角,求直线
为钝角,求直线 斜率
斜率 的取值范围;
的取值范围;
(3)过椭圆 上异于其顶点的任一点
上异于其顶点的任一点 作圆
作圆 :
: 的两条切线,切点分别为
的两条切线,切点分别为 (
( 不在坐标轴上),若直线
不在坐标轴上),若直线 在
在 轴、
轴、 轴上的截距分别为
轴上的截距分别为 、
、 ,证明:
,证明: 为定值.
为定值.
(本小题满分14分)定义在 的奇函数
的奇函数 有极小值为
有极小值为 .
.
(1)求 的解析式;
的解析式;
(2)若曲线 有三条不同的切线
有三条不同的切线 ,
, ,
, 相交于点
相交于点 ,求实数
,求实数 的取值范围.
的取值范围.