设函数
的定义域为
，则“
，
”是“函数
为增函数”的（ ）
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
已知函数
，则函数
的单调增区间是( )
A． |
B． |
C． |
D． 和 |
一个几何体的三视图如右图所示，则该几何体的表面积为（ ）
A． |
B． |
C． |
D． |
在边长为
的等边
中，
，
分别在边
与
上，且
，
，
则
（ ）
A． |
B． |
C． |
D． |
已知函数
，则不等式
的解集为（ ）
A． |
B． |
C． |
D． |
已知不等式组
，表示平面区域
，过区域中的任意一个点
，作圆
的两条切线且切点分别为
，
，当
最大时，点的坐标为的值为（ ）
A． |
B． |
C． |
D．无法确定 |
如图，椭圆的中心在坐标原点，焦点在
轴上，
，
，
，
为椭圆顶点，
为右焦点，延长
与
交于点
，若
为钝角，则该椭圆离心率的取值范围是（ ）
A． |
B． |
C． |
D． |
已知函数
，则关于
的方程
（相等的实数根算一个）的根的个数不可能为（ ）
| A．3 | B．4 | C．5 | D．6 |
方程
的解集为
，方程
的解集为
，且
，则
______，
_________．
在等差数列
中，
，
，则数列的通项公式为
_________，
已知实数
,函数
，当
时，则
_______，若
，则实数
的值为 ．
如图，在
中，
，
是
边上一点，
，
，
，则
的值为______，
的长为 ．
如图，在等腰三角形
中，已知
，
，
，
分别是边
，
上 的点，且
，
，其中
，
若
，
的中点分别为
，
，且 
则
的最小值是 ．
已知点
是双曲线
的左焦点，点
是该双曲线的右顶点，过点且垂直于
轴的直线与双曲线交于
，
两点，若
是锐角三角形，则该双曲线的离心率
的取值范围是________．
若关于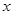
的不等式（组）
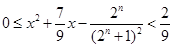对任意
恒成立，则所有这样的解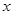构成的集合是____________．
设函数
（1）求
的最大值，并写出使取最大值时
的集合；
（2）已知
中，角
，
，
的对边分别为
，
，
，若
，
，求的最小值．
如图，在直三棱柱
中，平面
侧面
且
．
（1）求证：
；
（2）若直线
与平面所成的角为
，求锐二面角
的大小．
如图，在平面直角坐标系
中，离心率为
的椭圆
的左顶点为
，过原点
的直线（与坐标轴不重合）与椭圆
交于
两点，直线
分别与
轴交于
两点，若直线
斜率为时，
．
（1）求椭圆的标准方程；
（2）试问以
为直径的圆是否经过定点（与直线的斜率无关）？请证明你的结论．
已知
，数列
的前
项和为
，点
在曲线
上
且
，
．
（1）求数列的通项公式；
（2）数列
的前项和为且
满足
，试确定
的值，使得数列是等差数列；
（3）求证：
，
．
已知二次函数
．
（1）若对任意
，
，且
，都有
，求证：关于
的方程
有两个不相等的实数根且必有一个根属于
；
（2）若关于的方程
在上的根为
，且
，设函数
的图象的对称轴方程为
，求证：
．