设集合 ,
, 则
则 ( )
( )
A. |
B. |
C. |
D. |
命题“ 的否定是( )
的否定是( )
A. |
B. |
C. |
D. |
在复平面内,复数 与
与 的对应点关于原点对称,则
的对应点关于原点对称,则 ( )
( )
A. |
B. |
C. |
D. |
在等差数列 中,
中, ,前9项和
,前9项和 ,则其公差是( )
,则其公差是( )
A. |
B. |
C. |
D. |
某单位为了解用电量 (度)与气温
(度)与气温 之间的关系,随机统计了某
之间的关系,随机统计了某 天的用电量与当天气温,并制作了对照表:
天的用电量与当天气温,并制作了对照表:
气温 |
 |
 |
 |
 |
用电量 (度) (度) |
 |
 |
 |
 |
由表中数据得线性回归方程 ,预测当气温为
,预测当气温为 时,用电量的度数约为( ).
时,用电量的度数约为( ).
A. B.66 C.
B.66 C. D.68
D.68
某程序的框图如图所示,执行该程序,则输出的结果为( )

| A.7 | B.8 | C.9 | D.10 |
已知函数
 的部分图象如图所示,则函数
的部分图象如图所示,则函数 的解析式为( )
的解析式为( )

A. |
B. |
C. |
D. |
已知函数 ,若函数
,若函数 为奇函数,则
为奇函数,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
如果实数 满足:
满足: ,则
,则 的最大值是( )
的最大值是( )
| A.1 | B.2 | C.3 | D.4 |
函数 的图象大致是( )
的图象大致是( )

已知椭圆与双曲线的公共焦点为 ,椭圆与双曲线交于四点
,椭圆与双曲线交于四点 四点,若六边形
四点,若六边形 为正六边形,椭圆与双曲线的离心率分别为
为正六边形,椭圆与双曲线的离心率分别为 ,则( )
,则( )
| A.3 | B.2 | C.1 | D. |
已知:函数 的图象与函数
的图象与函数 (
( )的图象有一个交点,则
)的图象有一个交点,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知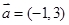 ,
,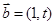 ,若
,若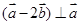 ,则
,则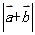
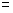 .
.
设数列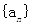 的前
的前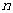 项和为
项和为 ,
,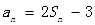 ,则
,则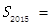 ;
;
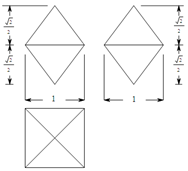
一个几何体的三视图如图所示,则这个几何体的外接球的表面积为 .
以抛物线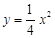 的焦点为圆心,以焦点到准线的距离为半径的圆被双曲线
的焦点为圆心,以焦点到准线的距离为半径的圆被双曲线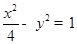 的
的
渐近线截得的弦长为 .
已知函数 (
( R)
R)
(1)求函数 的单调递减区间;
的单调递减区间;
(2)在 中角
中角 所对的边分别是
所对的边分别是 ,且
,且 ,
, ,
, ,
, 为锐角,求
为锐角,求 的值.
的值.
如图,在三棱柱 中,
中, 为棱
为棱 的中点,
的中点, ,
, .
.
求证:(1)
 平面
平面 ;
;
(2) ∥平面
∥平面 .
.
如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况,乙组某个数据的个位数模糊,记为 ,已知甲、乙两组的平均成绩相同.
,已知甲、乙两组的平均成绩相同.
(1)求 的值,并判断哪组学生成绩更稳定;
的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
(本小题满分12分)已知点 ,点
,点 是圆C:
是圆C: 上的任意一点,,线段
上的任意一点,,线段 的垂直平分线与直线
的垂直平分线与直线 交于点
交于点 .
.
(1)求点 的轨迹方程;
的轨迹方程;
(2)若直线 与点
与点 的轨迹有两个不同的交点
的轨迹有两个不同的交点 和
和 ,且原点
,且原点 总在以
总在以 为直径的圆的内部,求实数
为直径的圆的内部,求实数 的取值范围.
的取值范围.
已知函数 ,
, 
(Ⅰ) 时,证明:
时,证明: ;
;
(Ⅱ)若函数 没有零点,求实数
没有零点,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4-1:几何证明选讲
如图所示,AC为 的直径,D为
的直径,D为 的中点,E为BC的中点.
的中点,E为BC的中点.
(Ⅰ)求证:AB∥DE;
(Ⅱ)求证:2AD·CD=AC·BC.
(本小题满分10分)(本小题满分10分)选修:4-4:坐标系与参数方程
已知直线 (t为参数)经过椭圆
(t为参数)经过椭圆 (
( 为参数)的左焦点F.
为参数)的左焦点F.
(Ⅰ)求m的值;
(Ⅱ)设直线l与椭圆C交于A、B两点,求|FA|·|FB|的最大值和最小值.
(本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(1)解不等式 ;
;
(2)若 的最小值为
的最小值为 ,设
,设 且
且 求
求 的最小值;.
的最小值;.