设集合 ,
,
 ( )
( )
A. |
B. |
C. |
D. |
在复平面内,复数 与
与 的对应点关于原点对称,则
的对应点关于原点对称,则 ( )
( )
A. |
B. |
C. |
D. |
在等差数列 中,
中, ,前9项和
,前9项和 ,则其公差是( )
,则其公差是( )
A. |
B. |
C. |
D. |
某程序的框图如图所示,执行该程序,则输出的结果为( )

| A.7 | B.8 | C.9 | D.10 |
设 ,
, ,则( )
,则( )
A. |
B. |
C. |
D. |
已知函数
 的部分图象如图所示,则函数
的部分图象如图所示,则函数 的解析式为( )
的解析式为( )

A. |
B. |
C. |
D. |
已知函数 ,若函数
,若函数 为奇函数,则
为奇函数,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
如果实数 满足:
满足: ,则
,则 的最大值是( )
的最大值是( )
| A.1 | B.2 | C.3 | D.4 |
一次班级象棋比赛积分规则是:每人胜、平、负分别得2分、1分、0分,已知甲已赛3场,积3分,在这3场比赛中,甲胜、平、负(包括顺序)的情况共有( )
A. 种 种 |
B. 种 种 |
C. 种 种 |
D. 种 种 |
已知中心在坐标原点的椭圆和双曲线有公共焦点,且左、右焦点分别为 ,这两条曲线在第一象限的交点为
,这两条曲线在第一象限的交点为 是以
是以 为底边的等腰三角形。若
为底边的等腰三角形。若 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知:函数 的图象与函数
的图象与函数 (
( )的图象有一个交点,则
)的图象有一个交点,则 的取值范围是( ).
的取值范围是( ).
A. |
B. |
C. |
D. |
已知: 是函数
是函数 的两个极值点,且
的两个极值点,且 ,则直线
,则直线 与椭圆
与椭圆 的位置关系为( )
的位置关系为( )
| A.相切 | B.相交 | C.相离 | D.位置关系不确定 |
已知 ,
, ,若
,若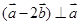 ,则
,则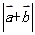
 .
.
设数列 的前
的前 项和为
项和为 ,
, ,则
,则 .
.
一个几何体的三视图如图所示,则这个几何体的外接球的表面积为

直线 分别与曲线
分别与曲线 ,
, 交于A,B,则
交于A,B,则 的最小值为 .
的最小值为 .
已知函数 (
( R)
R)
(1)求函数 的单调递减区间;
的单调递减区间;
(Ⅱ)在 中角
中角 所对的边分别是
所对的边分别是 ,且
,且 ,
, ,
, ,
, 为锐角,求
为锐角,求 的面积;
的面积;
如图,在斜三棱柱 中,侧面
中,侧面 与侧面
与侧面 都是菱形,
都是菱形, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求二面角
,求二面角 的余弦值.
的余弦值.
甲、乙、丙、丁四位好友约好出去游玩,为了增加乐趣,游玩的费用四人约好:每人掷一枚质地均匀的骰子决定出资的数值,掷出的点数为1或2的人出资200元,掷出的点数大于2的人出资100元;
(1)求这4个人中恰好有两人出资200元的概率;
(2)用 分别表示四个人出资200元、100元的人数,记
分别表示四个人出资200元、100元的人数,记 ,求
,求 的概率分布列和数学期望;
的概率分布列和数学期望;
椭圆
 (
( )的左焦点为
)的左焦点为 ,右焦点为
,右焦点为 ,离心率
,离心率 .设动直线
.设动直线
 与椭圆
与椭圆 相切于点
相切于点 且交直线
且交直线 于点
于点 ,
, 的周长为
的周长为 .
.
(1)求椭圆 的方程;
的方程;
(2)求证:以 为直径的圆恒过点
为直径的圆恒过点
已知函数 ,
, 
(Ⅰ) 时,证明:
时,证明: ;
;
(Ⅱ)若函数 没有零点,求实数
没有零点,求实数 的取值范围;
的取值范围;
(本小题满分10分)选修4-1:几何证明选讲
如图所示,AC为 的直径,D为
的直径,D为 的中点,E为BC的中点.
的中点,E为BC的中点.
(Ⅰ)求证:AB∥DE;
(Ⅱ)求证:2AD·CD=AC·BC.
(本小题满分10分)选修:4-4:坐标系与参数方程
已知直线 (t为参数)经过椭圆
(t为参数)经过椭圆 (
( 为参数)的左焦点F.
为参数)的左焦点F.
(Ⅰ)求m的值;
(Ⅱ)设直线l与椭圆C交于A、B两点,求|FA|·|FB|的最大值和最小值.
(本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(Ⅰ)解不等式 ;
;
(Ⅱ)若 的最小值为
的最小值为 ,设
,设 且
且 求
求 的最小值;.
的最小值;.