已知集合 ,则
,则








在复平面内复数 对应的点在
对应的点在 第一象限
第一象限 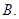 第二象限
第二象限  第三象限
第三象限  第四象限
第四象限
设函数 满足
满足 ,则
,则




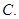
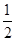
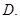
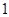
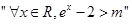 是
是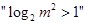 的
的 充分不必要条件
充分不必要条件  必要不充分条件
必要不充分条件  充要条件
充要条件 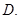 既不充分也不必要条件
既不充分也不必要条件
将函数 的图像向左平移
的图像向左平移 个单位后的图像关于原点对称,则函数
个单位后的图像关于原点对称,则函数 在
在 上的最小值为
上的最小值为







一个几何体的三视图及部分数据如图所示,侧视图为等腰三角形,俯视图为正方形,则这个几何体的体积为








设 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 成等比数列,则数列
成等比数列,则数列 的前
的前 项和
项和








执行如图程序在平面直角坐标系上打印一系列点,则打印出的点在圆 内的个数是
内的个数是








若双曲线 的渐近线与圆
的渐近线与圆 相离,则其离心率
相离,则其离心率 的取值范围是
的取值范围是







过抛物线 的焦点
的焦点 的直线
的直线 交抛物线
交抛物线 ,交其准线与点
,交其准线与点 ,若
,若 ,则抛物线的方程为
,则抛物线的方程为







设数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,则
,则 的取值范围是
的取值范围是







已知 满足条件
满足条件 ,则
,则 的最小值为
的最小值为
正三角形 的边长为
的边长为 ,将它沿高
,将它沿高 翻折,使点B与点C间的距离为
翻折,使点B与点C间的距离为 ,则四面体
,则四面体 的外接球的表面积为__________
的外接球的表面积为__________
在 中,若
中,若 ,则
,则 面积的最大值为__________
面积的最大值为__________
已知函数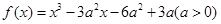 有且仅有一个零点
有且仅有一个零点 ,若
,若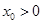 ,则
,则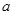 的取值范围是____________
的取值范围是____________
在 中,角
中,角 的对边分别是
的对边分别是 ,且
,且 。
。
(1)求证 。
。
(2)若 ,
, ,求
,求 的面积。
的面积。
如图,在直三棱柱 中,
中, ,
, ,
, 分别是
分别是 的中点。
的中点。
(1)求证 ;
;
(2)求点F到平面ABE的余距离。
某市现有居民 万人,每天有
万人,每天有 的人选择乘出租车出行,记每个人的乘车里程为
的人选择乘出租车出行,记每个人的乘车里程为 ,
, 。由调查数据得到
。由调查数据得到 的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程
的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程 时,乘车费用为
时,乘车费用为 元;当
元;当 时,每超出
时,每超出 (不足
(不足 时按
时按 计算),乘车费用增加
计算),乘车费用增加 元。
元。
(Ⅰ)试估计乘客的乘车费用不超过15.2元的概率;
(Ⅱ)试估计出租车公司一天的总收入是多小?(精确到 万元)
万元)
已知椭圆 的,离心率为
的,离心率为 ,
, 是其焦点,点
是其焦点,点 在椭圆上。
在椭圆上。
(Ⅰ)若 ,且
,且 的面积等于
的面积等于 。求椭圆的方程;
。求椭圆的方程;
(Ⅱ)直线 交椭圆于另一点
交椭圆于另一点 ,分别过点
,分别过点 作直线
作直线 的垂线,交
的垂线,交 轴于点
轴于点 ,当
,当 取最小值时,求直线
取最小值时,求直线 的斜率。
的斜率。
已知函数 曲线
曲线 在点
在点 处的切线方程为
处的切线方程为
(1),求 的值;
的值;
(2)求证:当 时,
时, 。
。
选修4-1:几何证明选讲
过以 为直径的圆上
为直径的圆上 点作直线交圆于
点作直线交圆于 点,交
点,交 挺长线于
挺长线于 点,过
点,过 点作圆的切线交
点作圆的切线交 于
于 点,交
点,交 挺长线于
挺长线于 点,且
点,且 。
。
(Ⅰ)求证 ;
;
(Ⅱ)设 为
为 的中点,求证
的中点,求证
选修4-4:坐标系与参数方程
在平面直角坐标系 中,
中, 是直线
是直线 上的一点,
上的一点, 是射线
是射线 上的一点,满足
上的一点,满足 。
。
(Ⅰ)求 点的轨迹;
点的轨迹;
(Ⅱ)设点 是(Ⅰ)中轨迹上任意一点,求
是(Ⅰ)中轨迹上任意一点,求 的最大值。
的最大值。
选修4-5:不等式选讲
设函数 ,
,
(Ⅰ)证明
(Ⅱ)若不等式 的解2集非空,求
的解2集非空,求 的取值范围。
的取值范围。