设全集U=R,
 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
函数 的图象大致为( )
的图象大致为( )

【改编】关于 的不等式
的不等式 的解集非空的充分不必要条件是( )
的解集非空的充分不必要条件是( )
A.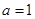 |
B.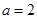 |
C.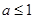 |
D.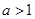 |
一个几何体的三视图如右图所示则,该几何体的体积为( )

A. |
B.1 | C. |
D. |
某程序框图如下左图所示,该程序运行后的 的值是( )
的值是( )

A. |
B. |
C. |
D. |
已知 和
和 是平面上的两个单位向量,且
是平面上的两个单位向量,且 ,
, ,若O为坐标原点,
,若O为坐标原点, 均为正常数,则
均为正常数,则 的最大值为 ( )
的最大值为 ( )
A. |
B. |
C. |
D. |
如果函数 满足:对于任意的
满足:对于任意的 ,都有
,都有 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
【改编】为了得到 的图象,只需将
的图象,只需将 的图象
的图象
A.把各点的横坐标缩短到原来的 倍,再向右平移 倍,再向右平移 个长度单位 个长度单位 |
B.把各点的横坐标缩短到原来的 倍,再向左平移 倍,再向左平移 个长度单位 个长度单位 |
C.把各点的横坐标缩短到原来的 倍,再向右平移 倍,再向右平移 个长度单位 个长度单位 |
D.把各点的横坐标缩短到原来的 倍,再向左平移 倍,再向左平移 个长度单位 个长度单位 |
【原创】有5个不同的红球和2个不同的黑球排成一列,在两端都有红球的排列中,其中红球甲和黑球乙相邻,且红球甲不在两端的排法有( )
| A.720 | B.576 | C.960 | D.1440 |
函数 ,其中
,其中 ,若动直线
,若动直线 与函数
与函数 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为 、
、 、
、 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知 为坐标原点,点
为坐标原点,点 .若点
.若点 为平面区域
为平面区域 上的动点,则
上的动点,则 的取值范围是 .
的取值范围是 .
【改编】若 的展开式中的常数项为112,则实数
的展开式中的常数项为112,则实数 _________.
_________.
【改编】已知等差数列 的前
的前 项和是
项和是 ,则使
,则使 的最小正整数
的最小正整数 等于 .
等于 .
若正数 ,
, 满足
满足 ,则
,则 的最小值为 .
的最小值为 .
对定义在区间D上的函数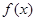 和
和 ,如果对任意
,如果对任意 ,都有
,都有 成立,那么称函数
成立,那么称函数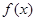 在区间D上可被
在区间D上可被 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
①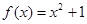 在区间
在区间 上可被
上可被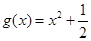 替代;
替代;
② 可被
可被 替代的一个“替代区间”为
替代的一个“替代区间”为 ;
;
③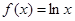 在区间
在区间 可被
可被 替代,则
替代,则 ;
;
④ ,则存在实数
,则存在实数 ,使得
,使得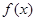 在区间
在区间 上被
上被 替代;
替代;
其中真命题的有
设函数
(Ⅰ)求 的最小正周期及值域;
的最小正周期及值域;
(Ⅱ)已知 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,求
,求 的面积.
的面积.
如图, 中,
中, 是
是 的中点,
的中点, ,
, .将
.将 沿
沿 折起,使
折起,使 点与图中
点与图中 点重合.
点重合.
(Ⅰ)求证: ;
;
(Ⅱ)当三棱锥 的体积取最大时,求二面角
的体积取最大时,求二面角 的余弦值;
的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试问在线段 上是否存在一点
上是否存在一点 ,使
,使 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ?证明你的结论.
?证明你的结论.
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图), 巷道有
巷道有 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是 ;
; 巷道有
巷道有 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为 .
.
(1)求 巷道中,三个易堵塞点最多有一个被堵塞的概率;
巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若 巷道中堵塞点个数为
巷道中堵塞点个数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
已知椭圆 经过点
经过点 ,其离心率为
,其离心率为 ,设直线
,设直线 与椭圆
与椭圆 相交于
相交于 两点.
两点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知直线 与圆
与圆 相切,求证:
相切,求证: (
( 为坐标原点);
为坐标原点);
(Ⅲ)以线段 为邻边作平行四边形
为邻边作平行四边形 ,若点
,若点 在椭圆
在椭圆 上,且满足
上,且满足 (
( 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围.
设 .
.
(1)令 ,求
,求 的单调区间;
的单调区间;
(2)若当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(本小题满分7分)选修4—2:矩阵与变换
如图,矩形 的
的 在变换
在变换 的作用下分别变成
的作用下分别变成 ,形成了平行四边形
,形成了平行四边形
(Ⅰ)求变换 对应的矩阵
对应的矩阵 ;
;
(Ⅱ)变换 对应的矩阵
对应的矩阵 将直线
将直线 变成了直线
变成了直线 :
: ,求直线
,求直线 的(1)方程.
的(1)方程.
(本小题满分7分)《选修4-4:坐标系与参数方程》
已知直线的极坐标方程为 ,圆
,圆 的参数方程为
的参数方程为 (其中
(其中 为参数).
为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
【改编】(本小题满分7分)选修4—5:不等式选讲
已知关于 的不等式:
的不等式: 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.
(Ⅰ)求整数 的值;
的值;
(Ⅱ)已知a,b,c∈R,若 ,求
,求 的最大值.
的最大值.