设全集 ,
, ,则图中阴影部分表示的集合是( )
,则图中阴影部分表示的集合是( )

| A.{1,3,5} | B.{1,2,3,4,5} | C.{7,9} | D.{2,4} |
下列命题正确的是( )
A.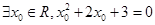 |
B.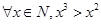 |
C.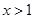 是 是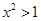 的充分不必要条件 的充分不必要条件 |
D.若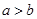 ,则 ,则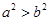 |
如图是一个空间几何体的三视图,这个几何体的体积是 ( )

A. |
B. |
C. |
D. |
 的三个顶点所对的复数分别为
的三个顶点所对的复数分别为 ,复数Z满足
,复数Z满足 ,则Z的对应点是
,则Z的对应点是 的( )
的( )
| A.外心 | B.内心 | C.重心 | D.垂心 |
执行如图所示的程序框图,若输出 的值为23,则输入的
的值为23,则输入的 值为 ( )
值为 ( )

| A.0 | B.1 | C.2 | D.11 |
函数 的图像可能是( )
的图像可能是( )

【原创】在平面直角坐标系 中,已知圆
中,已知圆 上有且仅有四个点到直线
上有且仅有四个点到直线 的距离为1,则实数
的距离为1,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
如图,已知直角三角形 的三边
的三边 的长度成等差数列,点
的长度成等差数列,点 为直角边AB的中点,点D在斜边AC上,且
为直角边AB的中点,点D在斜边AC上,且 ,若
,若 ,则
,则

A. |
B. |
C. |
D. |
【原创】福州某中学校园文化艺术节在2015年4月开幕,在其中一场次中,由二胡社,古筝社各表演两个节目,国学社表演一个节目,要求同社团的节目不相邻,节目单排法的种数是()
| A.72 | B.60 | C.48 | D.24 |
设定义在R上的偶函数 满足
满足 ,
, 是
是 的导函数,当
的导函数,当 时,
时, ;当
;当 且
且 时,
时, .则方程
.则方程 根的个数为( )
根的个数为( )
| A.12 | B.1 6 | C.18 | D.20 |
在区间 上随机取一个数
上随机取一个数 ,使得函数
,使得函数 有意义的概率为 .
有意义的概率为 .
【改编】已知 的展开式中
的展开式中 的系数是
的系数是 ,则
,则 __________.
__________.
对任意的实数 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .
把正整数按一定的规则排成了如图所示的三角形数表.

设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数,如
个数,如 .若
.若 ,则
,则 .
.
若函数 在
在 上的导函数为
上的导函数为 ,且不等式
,且不等式 恒成立,又常数
恒成立,又常数 ,满足
,满足 ,则下列不等式一定成立的是 .
,则下列不等式一定成立的是 .
① ;②
;② ;③
;③ ;④
;④ .
.
在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,向量
的对边,向量 ,
, ,且
,且 //
// .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)设 ,且
,且 的最小正周期为
的最小正周期为 ,求
,求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
【改编】如图,在直三棱柱 中,D、E分别为
中,D、E分别为 、AD的中点,F为
、AD的中点,F为 上的点,且
上的点,且

(Ⅰ)证明:EF∥平面ABC;
(Ⅱ)若 ,
, ,
,
(Ⅰ)求三棱锥 的体积;
的体积;
(Ⅱ)求二面角 的大小.
的大小.
如图所示,机器人海宝按照以下程序运行
①从A出发到达点B或C或D,到达点B、C、D之一就停止;
②每次只向右或向下按路线运行;
③在每个路口向下的概率 ;
;
④到达P时只向下,到达Q点只向右.
(1)求海宝过点从A经过M到点B的概率,求海宝过点从A经过N到点C的概率;
(2)记海宝到点B、C、D的事件分别记为X=1,X=2,X=3,求随机变量X的分布列及期望.
设椭圆 :
: 的左、右焦点分别是
的左、右焦点分别是 、
、 ,下顶点为
,下顶点为 ,线段
,线段 的中点为
的中点为 (
( 为坐标原点),如图.若抛物线
为坐标原点),如图.若抛物线 :
: 与
与 轴的交点为
轴的交点为 ,且经过
,且经过 、
、 两点.
两点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 ,
, 为抛物线
为抛物线 上的一动点,过点
上的一动点,过点 作抛物线
作抛物线 的切线交椭圆
的切线交椭圆 于
于 、
、 两点,求
两点,求 面积的最大值.
面积的最大值.
已知函数 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(Ⅰ)求函数 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若函数 对任意
对任意 满足
满足 ,求证:当
,求证:当 时,
时, ;
;
(Ⅲ)若 ,且
,且 ,求证:
,求证:
(本小题满分7分)选修4—2:矩阵与变换
如图,单位正方形区域 在二阶矩阵
在二阶矩阵 的作用下变成平行四边形
的作用下变成平行四边形 区域.
区域.
(Ⅰ)求矩阵 ;
;
(Ⅱ)求 ,并判断
,并判断 是否存在逆矩阵?若存在,求出它的逆矩阵.
是否存在逆矩阵?若存在,求出它的逆矩阵.
(本小题满分7分)《选修4-4:坐标系与参数方程》
在极坐标系中,圆 的极坐标方程为
的极坐标方程为 .现以极点
.现以极点 为原点,极轴为
为原点,极轴为 轴的非负半轴建立平面直角坐标系.
轴的非负半轴建立平面直角坐标系.
(Ⅰ)求圆 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若圆 上的动点
上的动点 的直角坐标为
的直角坐标为 ,求
,求 的最大值,并写出
的最大值,并写出 取得最大值时点P的直角坐标.
取得最大值时点P的直角坐标.
(本小题满分7分)选修4—5:不等式选讲
已知函数 ,
, ,且
,且 的解集为
的解集为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,且
,且 ,求
,求  的最小值.
的最小值.