已知集合 ,
, 为虚数单位,
为虚数单位, ,若
,若 ,则复数
,则复数 的共轭复数
的共轭复数 的虚部是( )
的虚部是( )
A. |
B. |
C. |
D. |
【原创】设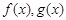 是定义在
是定义在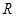 上的函数,
上的函数, ,则“
,则“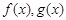 均为奇函数”是“
均为奇函数”是“ 为偶函数”的( )
为偶函数”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
设 ,则
,则 =
=
A. |
B. |
C.5 | D. |
函数 与
与 在同一平面直角坐标系内的大致图象为( )
在同一平面直角坐标系内的大致图象为( )
A. |
B. |
C. |
D. |
【改编】若函数 在区间
在区间 上单调递增,在区间
上单调递增,在区间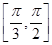 上单调递减,则关于
上单调递减,则关于 说法正确的是( )
说法正确的是( )
A.对称中心是 |
B.对称轴是 |
C.对称中心是 |
D.对称轴是 |
已知向量 不共线,向量
不共线,向量 ,则下列命题正确的是
,则下列命题正确的是
A.若 为定值,则 为定值,则 三点共线. 三点共线. |
B.若 ,则点 ,则点 在 在 的平分线所在直线上. 的平分线所在直线上. |
C.若点 为 为 的重心,则 的重心,则 . . |
D.若点 在 在 的内部(不含边界),则 的内部(不含边界),则 . . |
已知数列 的首项为
的首项为 ,且满足对任意的
,且满足对任意的 ,都有
,都有 ,
, 成立,则
成立,则 ( )
( )
A. |
B. |
C. |
D. |
【改编】已知x,y满足 ,则
,则 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
已知 ,椭圆
,椭圆 的方程为
的方程为 ,双曲线
,双曲线 的方程为
的方程为 ,
, 与
与 的离心率之积为
的离心率之积为 ,则
,则 的渐近线方程为( )
的渐近线方程为( )
A. |
B. |
C. |
D. |
若定义在R上的函数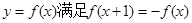 满足,且当
满足,且当 时,
时,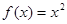 ,函数
,函数 ,则函数
,则函数 在区间
在区间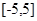 内的零点的个数为( )
内的零点的个数为( )
| A.6 | B.7 | C.8 | D.9 |
已知 ,
, 若
若 ,则实数
,则实数 .
.
如图, 是以
是以 为圆心,半径为
为圆心,半径为 的圆的内接正方形.将一颗豆子随机地扔到该圆内,用
的圆的内接正方形.将一颗豆子随机地扔到该圆内,用 表示事件“豆子落在正方形
表示事件“豆子落在正方形 内”,
内”, 表示事件“豆子落在扇形
表示事件“豆子落在扇形 (阴影部分)内”,则
(阴影部分)内”,则 .
.

【改编】已知直线 与x轴相交于点A,与y轴相交于点B,且以坐标原点为圆心以
与x轴相交于点A,与y轴相交于点B,且以坐标原点为圆心以 为半径的圆与直线l相切,若△AOB面积为
为半径的圆与直线l相切,若△AOB面积为 ,则
,则 _____________.
_____________.
若关于x的不等式(组) 恒成立,则所有这样的解x构成的集合是____________.
恒成立,则所有这样的解x构成的集合是____________.
以下四个关于圆锥曲线的命题中:
①设 为两个定点,
为两个定点, 为非零常数,
为非零常数, ,则动点
,则动点 的轨迹为双曲线;
的轨迹为双曲线;
②已知圆 上一定点
上一定点 和一动点
和一动点 ,
, 为坐标原点,若
为坐标原点,若 则动点
则动点 的轨迹为圆;
的轨迹为圆;
③ ,则双曲线
,则双曲线 与
与 的离心率相同;
的离心率相同;
④已知两定点 和一动点
和一动点 ,若
,若 ,则点
,则点 的轨迹关于原点对称.
的轨迹关于原点对称.
其中真命题的序号为 (写出所有真命题的序号).
已知向量 ,
, ,函数
,函数 .
.
(1)求函数 的最小正周期
的最小正周期 与值域;
与值域;
(2)已知 ,
, ,
, 分别为
分别为 内角
内角 ,
,  ,
, 的对边,其中
的对边,其中 为锐角,
为锐角, ,
, ,且
,且 ,求
,求 ,
, 和
和 的面积
的面积 .
.
如图,三棱柱 中,
中, ,
, ,平面
,平面 平面
平面 ,
, 与
与 相交于点
相交于点 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
已知椭圆 的方程为
的方程为 ,双曲线
,双曲线 的左、右焦点分别为
的左、右焦点分别为 的左、右顶点,而
的左、右顶点,而 的左、右顶点分别是
的左、右顶点分别是 的左、右焦点。
的左、右焦点。
(1)求双曲线 的方程;
的方程;
(2)若直线 与椭圆
与椭圆 及双曲线
及双曲线 都恒有两个不同的交点,且L与的两个焦点A和B满足
都恒有两个不同的交点,且L与的两个焦点A和B满足 (其中O为原点),求
(其中O为原点),求 的取值范围。
的取值范围。
【改编】已知函数 (
( 是常数)在
是常数)在 处的切线方程为
处的切线方程为 ,且
,且 .
.
(Ⅰ)求常数 的值;
的值;
(Ⅱ)若函数 (
( )在区间
)在区间 内不是单调函数,求实数
内不是单调函数,求实数 的取值范围;
的取值范围;
(Ⅲ)证明: .
.
(本小题满分7分)选修4—2:矩阵与变换
已知矩阵
(Ⅰ)求A的逆矩阵A-1;
(Ⅱ)求A的特征值及对应的特征向量。
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆 的极坐标方程;
的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 的交点为
的交点为 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
(本小题满分7分)选修4—5:不等式选讲
已知函数 ,
, , 若
, 若
 恒成立,实数
恒成立,实数 的最大值为
的最大值为 .
.
(Ⅰ)求实数 .
.
(Ⅱ)已知实数 满足
满足 且
且 的最大值是
的最大值是 ,求
,求 的值.
的值.