已知集合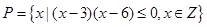 ,
,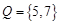 ,下列结论成立的是( )
,下列结论成立的是( )
A.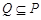 |
B.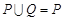 |
C.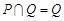 |
D.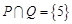 |
【改编】设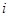 为虚数单位,若复数
为虚数单位,若复数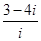 与复数
与复数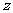 在复平面内对应的点关于虚轴对称,则
在复平面内对应的点关于虚轴对称,则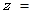 ( )
( )
A.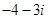 |
B.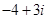 |
C.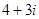 |
D.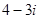 |
命题P: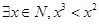 ;命题q:
;命题q: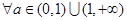 ,函数
,函数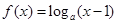 的图象过点
的图象过点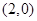 ,则( )
,则( )
| A.P假q真 | B.P真q假 | C.P假q假 | D.P真q真 |
【原创】设x,y满足约束条件 ,则
,则 的最大值为( )
的最大值为( )
A. |
B.3 | C.2 | D. |
设 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
在直角梯形ABCD中,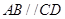 ,
,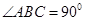 ,
, ,则
,则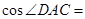 ( )
( )
A.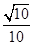 |
B.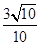 |
C. |
D. |
阅读如右图所示的程序框图,则该算法的功能是( )
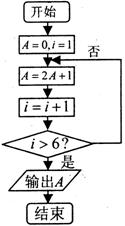
A.计算数列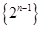 前 前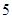 项的和 项的和 |
B.计算数列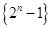 前 前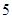 项的和 项的和 |
C.计算数列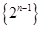 前 前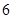 项的和 项的和 |
D.计算数列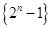 前 前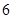 项的和 项的和 |
设函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当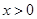 时,
时,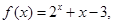 则
则 的零点个数为( )
的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
已知 ,
,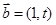 ,若
,若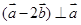 ,则
,则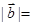 .
.
一个几何体的三视图如图所示,则该几何体的体积为

【改编】若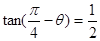 ,则
,则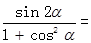 ;
;
二项式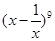 的展开式中的
的展开式中的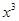 系数是_________(用数字作答)
系数是_________(用数字作答)
设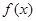 是定义在
是定义在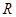 上的偶函数,对任意
上的偶函数,对任意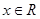 ,都有
,都有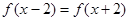 ,且当
,且当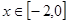 时,
时,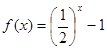 .若函数
.若函数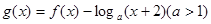 在区间
在区间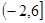 恰有3个不同的零点,则
恰有3个不同的零点,则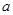 的取值范围是 .
的取值范围是 .
(极坐标与参数方程)已知直线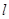 的参数方程:
的参数方程: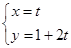 (
(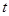 为参数)和圆
为参数)和圆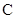 的极坐标方程:
的极坐标方程: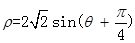 ,则直线
,则直线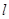 被圆截得的弦长为 ;
被圆截得的弦长为 ;
(几何证明选讲选做题)如图,BE、CF分别为钝角△ABC的两条高,已知
 则BC边的长为 .
则BC边的长为 .

【改编】(本小题满分12分)已知函数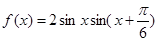 .
.
(1)当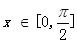 时,求函数
时,求函数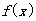 的最大值;
的最大值;
(2)当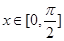 时,求函数
时,求函数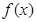 的单调增区间;
的单调增区间;
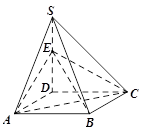
(本小题满分12分)如图,四棱锥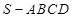 的底面是正方形,
的底面是正方形,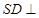 平面
平面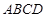 ,
,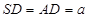 ,点
,点 是
是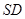 上的点,且
上的点,且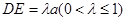 .
.
(1)求证:对任意的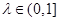 ,都有
,都有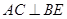 ;
;
(2)若二面角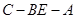 的大小为
的大小为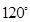 ,求实数
,求实数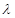 的值.
的值.
【原创】(本小题满分14分)据报道,中国经济虽然有所下滑,但仍处于可控状态,从中央到地方对中国经济都抱有信心,因此股市的上证指数从去年的低点1974.38,涨到今天3286.07,为了了解股民的收益状况,某证券公司随机抽取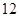 位股民目前的战绩情况,数据显示这些股民的收益目前在所有股民中所占的百分数据,用茎叶图形式表示如下:
位股民目前的战绩情况,数据显示这些股民的收益目前在所有股民中所占的百分数据,用茎叶图形式表示如下: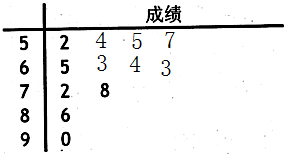
根据百分数据,成绩不低于80的为市场赢家.
(1)将频率视为概率,根据样本估计总体的思想,在股民中任选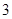 人,求至少有
人,求至少有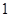 人为“市场赢家”的概率;
人为“市场赢家”的概率;
(2)从抽取的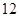 人中随机选取
人中随机选取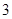 人,记
人,记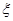 表示“市场赢家”人数,求
表示“市场赢家”人数,求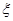 的分布列及期望.
的分布列及期望.
(本小题满分14分)已知各项不为零的数列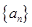 的前
的前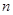 项和为
项和为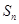 ,且满足
,且满足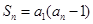 .
.
(1)求数列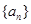 的通项公式;
的通项公式;
(2)设数列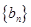 满足
满足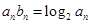 ,求数列
,求数列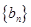 的前
的前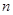 项和
项和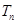 .
.
已知抛物线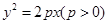 的焦点为F,点P是抛物线上的一点,且其纵坐标为4,
的焦点为F,点P是抛物线上的一点,且其纵坐标为4,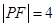 .
.
(1)求抛物线的方程;
(2)设点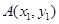 ,
,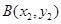 (
(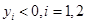 )是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
)是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
(本小题满分12分)已知函数 ,
, .
.
(Ⅰ) 时,证明:
时,证明: ;
;
(Ⅱ) ,若
,若 ,求a的取值范围.
,求a的取值范围.