已知集合
，集合
，
，则
（ ）
A． |
B． |
C． |
D． |
i为虚数单位，
， 则
的共轭复数为 （ ）
| A．2-i | B．2+i | C．-2-i | D．-2+i |
设
是等差数列，若
，则数列前8项和为（ ）
A． |
B．80 | C．64 | D．56 |
某中学进行模拟考试有80个考场，每个考场30个考生，每个考生座位号按1～30号随机编排，每个考场抽取座位号为15号考生试卷评分，这种抽样方法是（ ）
| A．简单随机抽样 | B．系统抽样 | C．分层抽样 | D．分组抽样 |
已知向量
，
，则
的充要条件是（ ）
A． |
B． |
C． |
D． |
【原创】若
，则有（ ）.
A． |
B． |
C． |
D． |
为得到函数
的图象，可将函数
的图象向左平移
个单位长度，或向右平移
个单位长度（，均为正整数），则
的最小值是（ ）
A． |
B． |
C． |
D． |
【原创】已知实数
、
满足不等式组
，则复数
的模的最大值为是（ ）
A． |
B． |
C． |
D． |
已知函数
，则曲线
在点
处的切线方程为___________.
二项式
的展开式中的
系数是_________（用数字作答）
【原创】先研究函数
的单调性，然后把
、
比较大小，按从小到大的顺序依次为 （用不等式形式书写）；
已知
，若
是它一条对称轴，则 
．
在
中，角
所对的边分别为
，若
且
，则面积的最大值为 ．
如图，
是圆
的直径，点
在圆上，延长
到
使
，过作圆的切线交
于
.若
，
则
_________.
在极坐标系中，圆
的圆心到直线
的距离是
【改编】设函数
.
（1）求
的定义域和最小正周期；
（2）当
，若
成立，求
的取值范围；
某中学将
名高一新生分成水平相同的甲、乙两个“平行班”，每班
人，吴老师采用
、
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果，期末考试后，分别从两个班级中各随机抽取
名学生的成绩进行统计，作出的茎叶图如下：
记成绩不低于
分者为“成绩优秀”.
（1）在乙班样本的个个体中，从不低于
分的成绩中随机抽取
个，记随机变量
为抽到“成绩优秀”的个数，求的分布列及数学期望
；
（2）由以上统计数据填写下面
列联表，并判断有多大把握认为“成绩优秀”与教学方式有关？
| |
甲班（方式） |
乙班（方式） |
总计 |
| 成绩优秀 |
|
|
|
| 成绩不优秀 |
|
|
|
| 总计 |
|
|
|
（本小题满分14分）设
表示数列
的前
项和.
（1）若为公比为
的等比数列，写出并推导的计算公式;
（2）若
，
，求证：
<1.
（本小题满分14分）如图，四棱锥
中，
，底面
为梯形，
，
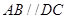，且
，
.
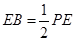（1）求证：
;
（2）求二面角
的余弦值.
（本小题满分14分）已知椭圆
（
）的离心率为
，右焦点到直线
的距离为
.
（1）求椭圆
的方程；
（2）已知点
，斜率为
的直线
交椭圆于两个不同点
. 
，设直线
与
的斜率分别为
，
，
①若直线过椭圆的左顶点，求此时，的值；
②试猜测，的关系，并给出你的证明.
（本小题满分14分）已知
，函数
，
．（
的图象连续不断）
（Ⅰ） 求的单调区间；
（Ⅱ） 当
时，证明：存在
，使
；
（Ⅲ） 若存在属于区间
的
，且
，使
，证明：
．