集合A={-1,0,2},B={x||x|<1},则A B=
B=
【原创】已知复数 (
( 为虚数单位,
为虚数单位, ),则其虚部为 .
),则其虚部为 .
甲、乙两位同学下棋,若甲获胜的概率为 ,甲、乙下和棋的概率为
,甲、乙下和棋的概率为 ,则乙获胜的概率为 .
,则乙获胜的概率为 .
如图是一个算法流程图,输出的结果为

若数据 的方差为
的方差为 ,则
,则 .
.
若双曲线 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 ,则该双曲线的渐近线方程是 .
,则该双曲线的渐近线方程是 .
若一个圆锥的底面半径为 ,侧面积是底面积的
,侧面积是底面积的 倍,则该圆锥的体积为 .
倍,则该圆锥的体积为 .
已知函数 的定义域是
的定义域是 ,则实数
,则实数 的值为 .
的值为 .
将函数  的图象分别向左、向右各平移
的图象分别向左、向右各平移 个单位长度后,所得的两个图象对称轴重合,则
个单位长度后,所得的两个图象对称轴重合,则  的最小值为______.
的最小值为______.
设等比数列 的公比为
的公比为 (
( ),前n项和为
),前n项和为 ,若
,若 ,且
,且 与
与 的等差中项为
的等差中项为 ,则
,则 .
.
如图,在 中,已知
中,已知 ,点
,点 分别在边
分别在边 上,且
上,且 ,点
,点 为
为 中点,则
中点,则 的值为 .
的值为 .

【原创】已知椭圆 的左焦点为
的左焦点为 ,直线
,直线 与椭圆相交于
与椭圆相交于 两点.若
两点.若 的周长最大时,
的周长最大时, 的面积为
的面积为 则椭圆的离心率为
则椭圆的离心率为
【原创】已知 ,若
,若 互不相等,且满足
互不相等,且满足 ,则
,则 的取值范围是 .
的取值范围是 .
【原创】已知函数 .若存在常数
.若存在常数 ,满足:对任意的
,满足:对任意的 ,都存在
,都存在 ,使得
,使得 ,则常数m是 .
,则常数m是 .
【原创】(本小题满分14分)设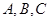 是单位圆上三点,
是单位圆上三点,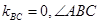 为锐角.
为锐角.
(1)若 求
求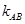
(2)若 求三角形
求三角形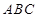 面积的最大值.
面积的最大值.
如图,在正方体 中,
中, 分别是
分别是 中点.
中点.
求证:(1) ∥平面
∥平面 ;
;
(2) 平面
平面 .
.
(本小题满分15分)某飞机失联,经卫星侦查,其最后出现在小岛 附近.现派出四艘搜救船
附近.现派出四艘搜救船 ,为方便联络,船
,为方便联络,船 始终在以小岛
始终在以小岛 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船 构成正方形编队展开搜索,小岛
构成正方形编队展开搜索,小岛 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛 到
到 的距离为
的距离为 ,
, 船到小岛
船到小岛 的距离为
的距离为 .
.
(1)请分别求 关于
关于 的函数关系式
的函数关系式 ;并分别写出定义域;
;并分别写出定义域;
(2)当 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即 最大).
最大).
如图,在平面直角坐标系 中,离心率为
中,离心率为 的椭圆
的椭圆
 的左顶点为
的左顶点为 ,过原点
,过原点 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆 交于
交于 两点,直线
两点,直线 分别与
分别与 轴交于
轴交于 两点.若直线
两点.若直线 斜率为
斜率为 时,
时, .
.

(1)求椭圆 的标准方程;
的标准方程;
(2)试问以 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
已知数列 中
中
 .
.
(1)是否存在实数 ,使数列
,使数列 是等比数列?若存在,求
是等比数列?若存在,求 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)若 是数列
是数列 的前
的前 项和,求满足
项和,求满足 的所有正整数
的所有正整数 .
.
已知函数 。
。
(1)若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值。
(2)若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由;
(3)若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x 时,恒有f(x)>g(x)成立。
时,恒有f(x)>g(x)成立。
如图,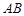 ,
, 是半径为
是半径为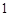 的圆
的圆 的两条弦,它们相交于
的两条弦,它们相交于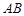 的中点
的中点 ,若
,若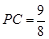 ,
, 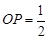 ,求
,求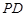 的长.
的长.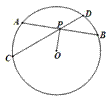
【原创】选修4-2:矩阵与变换(本小题满分10分)
设二阶矩阵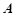 ,
,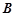 满足
满足 ,
,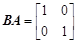 ,求
,求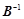 ..
..
(本小题满分10分,坐标系与参数方程选讲)
己知在平面直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为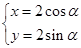 (
(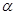 为参数).以原点
为参数).以原点 为极点,以
为极点,以 轴的非负半轴为极轴的极坐标系中,直线
轴的非负半轴为极轴的极坐标系中,直线 的极坐标方程为
的极坐标方程为 ,直线
,直线 与圆
与圆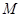 相交于
相交于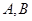 两点,求弦
两点,求弦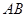 的长.
的长.
【原创】已知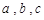 均为正数,证明:
均为正数,证明: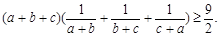
如图,在直三棱柱 中,
中, ,
, ,
, ,动点
,动点 满足
满足 ,当
,当 时,
时, .
.
(1)求棱 的长;
的长;
(2)若二面角 的大小为
的大小为 ,求
,求 的值..
的值..
(本小题满分10分) 记 为从
为从 个不同的元素中取出
个不同的元素中取出 个元素的所有组合的个数.随机变量
个元素的所有组合的个数.随机变量 表示满足
表示满足 的二元数组
的二元数组 中的
中的 ,其中
,其中 ,每一个
,每一个 (
( 0,1,2, ,
0,1,2, , )都等可能出现.求
)都等可能出现.求 .
.