已知i是虚数单位,则 的实部为
的实部为
设全集 ,集合
,集合 ,则
,则 = .
= .
执行如图所示的流程图,则输出的 为 .
为 .

某中学共有学生 人,其中高一年级
人,其中高一年级 人,高二年级
人,高二年级 人,高三年级
人,高三年级 人,现采用分层抽样的方法,抽取
人,现采用分层抽样的方法,抽取 人进行体育达标检测,则抽取高二年级学生人数为 .
人进行体育达标检测,则抽取高二年级学生人数为 .
【原创】甲乙丙丁四人玩传球游戏,第一次,甲传给乙丙丁三人中任意一人,第二次由拿球者再传给其他三人中任意一人,这样共传了四次,则第四次仍传回到甲的概率等于 .
【原创】设双曲线 的右焦点为F,M是双曲线上任意一点,点A(9,2),则
的右焦点为F,M是双曲线上任意一点,点A(9,2),则 的最小值为 .
的最小值为 .
在等差数列 中,已知
中,已知 ,则
,则 的值为______.
的值为______.
实数x,y满足 ,则
,则 的最小值为
的最小值为
已知直线 过点
过点 且与圆
且与圆 相交于
相交于 两点,
两点, 的面积为1,则直线
的面积为1,则直线 的方程为 .
的方程为 .
底面边长为 ,高为
,高为 的正四棱锥的侧面积为 .
的正四棱锥的侧面积为 .
若函数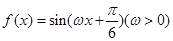 图象的两条相邻的对称轴之间的距离为
图象的两条相邻的对称轴之间的距离为 ,且该函数图象关于点
,且该函数图象关于点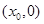 成中心对称,
成中心对称,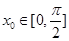 ,则
,则 .
.
已知向量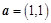 ,
,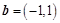 ,设向量
,设向量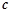 满足
满足 ,则
,则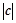 的最大值为 .
的最大值为 .
【原创】已知二次函数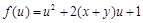 的值域为
的值域为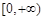 ,且当
,且当 ,
,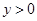 时,不等式
时,不等式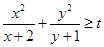 恒成立,则实数
恒成立,则实数 的最大值为 .
的最大值为 .
【原创】设椭圆方程为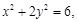 若过定圆C上每一点都可以作与椭圆相切的两条互相垂直的直线,则圆C的方程为_ __ .
若过定圆C上每一点都可以作与椭圆相切的两条互相垂直的直线,则圆C的方程为_ __ .
已知向量 ,且
,且 共线,其中
共线,其中 .
.
(1)求 的值;
的值;
(2)若 ,求
,求 的值.
的值.
(本小题满分14分)如图,四棱锥 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD,PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD,PB=PD, ⊥
⊥ ,
, ⊥
⊥ ,
, ,
, 分别是
分别是 ,
, 的中点,连结
的中点,连结 .
.
求证:(1) ∥平面
∥平面 ;
;
(2) ⊥平面
⊥平面 .
.
某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到 元.公司拟投入
元.公司拟投入 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
【原创】(本小题满分16分)在平面直角坐标系 中,椭圆
中,椭圆 过点
过点 ,一条准线方程为
,一条准线方程为 .线段
.线段  是过左焦点
是过左焦点  且不与
且不与 轴垂直的焦点弦.
轴垂直的焦点弦.
(1)求椭圆的方程及离心率;
(2)在左准线上是否存在点 ,使
,使 为正三角形.
为正三角形.
已知函数 (
( 为常数),其图象是曲线
为常数),其图象是曲线 .
.
(1)当 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(2)设函数 的导函数为
的导函数为 ,若存在唯一的实数
,若存在唯一的实数 ,使得
,使得 与
与 同时成立,求实数
同时成立,求实数 的取值范围;
的取值范围;
(3)已知点 为曲线
为曲线 上的动点,在点
上的动点,在点 处作曲线
处作曲线 的切线
的切线 与曲线
与曲线 交于另一点
交于另一点 ,在点
,在点 处作曲线
处作曲线 的切线
的切线 ,设切线
,设切线 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分16分)已知数列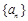 (
(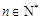 ,
,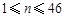 )满足
)满足 ,
,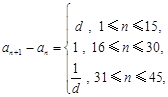 其中
其中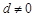 ,
,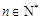 .
.
(1)当 时,求
时,求 关于
关于 的表达式,并求
的表达式,并求 的取值范围;
的取值范围;
(2)设集合 .
.
①若 ,
,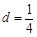 ,求证:
,求证: ;
;
②是否存在实数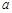 ,
, ,使
,使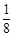 ,
,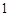 ,
,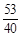 都属于
都属于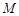 ?若存在,请求出实数
?若存在,请求出实数 ,
, ;若不存在,请说明理由.
;若不存在,请说明理由.
(选修4—1:几何证明选讲)如图,点 为锐角
为锐角 的内切圆圆心,过点
的内切圆圆心,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,圆
,圆 与边
与边 相切于点
相切于点 .若
.若 ,求
,求 的度数.
的度数.
选修4—2:矩阵与变换
已知矩阵 满足:
满足: ,其中
,其中 是互不相等的实常数,
是互不相等的实常数, 是非零的平面列向量,
是非零的平面列向量, ,
, ,求矩阵
,求矩阵 .
.
选修4-4:坐标系与参数方程(本小题满分10分)
在极坐标系中,已知圆 与直线
与直线 相切,求实数a的值.
相切,求实数a的值.
(选修4—5:不等式证明选讲)已知 均为正数,证明:
均为正数,证明: .
.
【原创】(本小题满分10分)从棱长为1的正方体的8个顶点中任取3个点,设随机变量ξ是以这三点为顶点的三角形的面积.
(1)求概率 ;
;
(2)求ξ的分布列,并求其数学期望E(ξ ).
设 是给定的正整数,有序数组(
是给定的正整数,有序数组( )中
)中 或
或
 .
.
(1)求满足“对任意的 ,
, ,都有
,都有 ”的有序数组(
”的有序数组( )的个数
)的个数 ;
;
(2)若对任意的 ,
, ,
, ,都有
,都有 成立,求满足“存在
成立,求满足“存在 ,使得
,使得 ”的有序数组(
”的有序数组( )的个数
)的个数